Question

A circular park of radius 20m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in their hands to talk to each other. Find the length of the string of each phone.

Answer 1

Hint: In order to solve this problem draw a rough diagram of an equilateral triangle inscribed in a circle of radius 20m then use the concept that the centre of a circle coincides with the centroid of the equilateral triangle which is inscribed in it. Then solve further to get the length of the side of that equilateral triangle.

Complete Step-by-Step solution:
Since three boys are at equal distance from each other which is only possible when they are in equilateral triangle and the ground is circular so the triangle will be inscribed in the circle of radius 20m.
The rough diagram to this question can be drawn as:

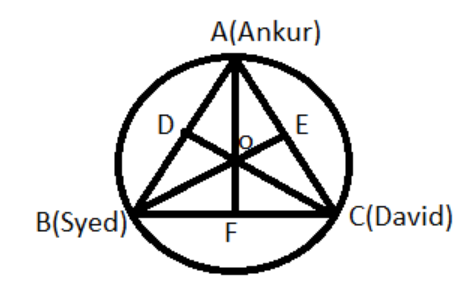
We have drawn the medians from all the vertices.
We know that the median divide the base in two equal parts and is also perpendicular to it in an equilateral triangle and its centroid coincides with the center of the circle which is on its vertices………………..(1)
We also know that the centroid of an equilateral triangle divide the median in the ratio 2:1.
So, we can say $\dfrac{{{\text{AO}}}}{{{\text{OF}}}}{\text{ = }}\dfrac{{\text{2}}}{{\text{1}}}$
We know AO is the radius of the circle which is 20m.
So,
$
  \dfrac{{{\text{AO}}}}{{{\text{OF}}}}{\text{ = }}\dfrac{{\text{2}}}{{\text{1}}}{\text{ = }}\dfrac{{{\text{20}}}}{{{\text{OF}}}} \\
  {\text{OF = 10m}} \\
$
On applying Pythagoras theorem in triangle BOF we get,
${\text{B}}{{\text{O}}^{\text{2}}}{\text{ = B}}{{\text{F}}^{\text{2}}}{\text{ + O}}{{\text{F}}^{\text{2}}}$
BO is the radius 20m and OF = 10m (calculated above)
$
  {\text{2}}{{\text{0}}^{\text{2}}}{\text{ = B}}{{\text{F}}^{\text{2}}}{\text{ + 1}}{{\text{0}}^{\text{2}}} \\
  {\text{400 = B}}{{\text{F}}^{\text{2}}}{\text{ + 100}} \\
  {\text{BF = }}\sqrt {{\text{300}}} {\text{ = 10}}\sqrt {\text{3}} \\
$
Hence, BF = $10\sqrt 3 $
And we know from 1 that F is the midpoint of BC so BC = 2BF=$20\sqrt 3 m$.
So, AB=BC=CA=$20\sqrt 3 m$.
So, the boys are $20\sqrt 3 m$ apart from each other.

Note: To solve this problem we need to consider the three boys sitting on the vertices of an equilateral triangle and we need the help of radius of the circle so we have inscribed the triangle in the circle. Also the ground is circular. Then we have used the properties of an equilateral triangle inscribed in a circle. Then applied Pythagoras theorem to get very close to the answer and used the concept that the median bisects the side of an equilateral triangle. Proceeding like this you will get the right answer.