Question

A circular lamina of radius a and centre O has a mass per unit area of $k{x^2}$ , where x is the distance from O and k is a constant. If the mass of the lamina is; in terms of M and a the moment of inertia of the lamina about an axis through O and perpendicular to the lamina is $I = \dfrac{x}{3}M{a^2}$. Find x.

Answer 1

Hint: In order to find the moment of inertia of the given shape, we need the mass of the lamina to find the moment of inertia, so we will consider mass of a small element and in order to find the mass of the lamina we will integrate the mass for the element. Further we will use the formula of moment of inertia and finally compare with the given value.

Formula used- \[M = \int\limits_0^a {dm} ,I = \int\limits_0^a {\left( {dm.{x^2}} \right)} \]

Complete Step-by-Step solution:
Let's consider the small element of lamina at x distance from the centre of thickness dx as shown below.

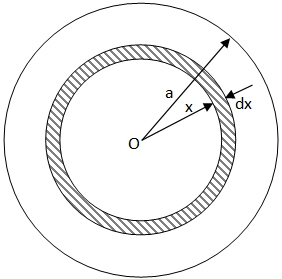
The area of the element is
$dA = 2\pi xdx$
The mass per unit area is given as
$\dfrac{{dm}}{{dA}} = k{x^2}$
The mass of lamina is,
\[
  M = \int\limits_0^a {dm} \\
   \Rightarrow M = \int\limits_0^a {k{x^2}.dA} \\
   \Rightarrow M = \int\limits_0^a {k{x^2}.\left( {2\pi xdx} \right)} \\
   \Rightarrow M = \int\limits_0^a {2\pi k{x^3}.dx} \\
   \Rightarrow M = 2\pi k\left[ {\dfrac{{{x^4}}}{4}} \right]_0^a \\
   \Rightarrow M = \dfrac{{\pi k{a^4}}}{2} \\
 \]
The moment of inertia of lamina about an axis through O and perpendicular to the lamina is,
\[
  I = \int\limits_0^a {\left( {dm.{x^2}} \right)} \\
   \Rightarrow I = \int\limits_0^a {\left( {k{x^2}dA.{x^2}} \right)} \\
   \Rightarrow I = \int\limits_0^a {\left( {k{x^4}dA} \right)} \\
   \Rightarrow I = \int\limits_0^a {\left( {k{x^4}\left( {2\pi xdx} \right)} \right)} \\
   \Rightarrow I = 2\pi k\int\limits_0^a {{x^5}.dx} \\
 \]
Solve further,
$
  I = 2\pi k\left[ {\dfrac{{{x^6}}}{6}} \right]_0^a \\
   \Rightarrow I = \dfrac{{\pi k{a^6}}}{3} \\
 $
As we know that:
\[
  \because M = \dfrac{{\pi k{a^4}}}{2} \\
   \Rightarrow k = \dfrac{{2M}}{{\pi {a^4}}} \\
 \]
Let us substitute the value of k in the equation of moment of inertia.
$
  \because I = \dfrac{{\pi k{a^6}}}{3} \\
   \Rightarrow I = \dfrac{{\pi \left( {\dfrac{{2M}}{{\pi {a^4}}}} \right){a^6}}}{3} \\
   \Rightarrow I = \dfrac{2}{3}M{a^2} \\
 $
Thus, the required moment of inertia is $\dfrac{2}{3}M{a^2}$
Hence, the value of x is 2.

Note- The moment of inertia of a solid body, otherwise known as the mass moment of inertia, angular momentum, or rotational inertia, is a quantity that specifies the torque necessary for a desired angular acceleration along a rotational axis; analogous to how gravity decides the force required for a desired acceleration. Students must remember the formula for moment of inertia for some common shapes and the general formula to find the moment of inertia.