Question

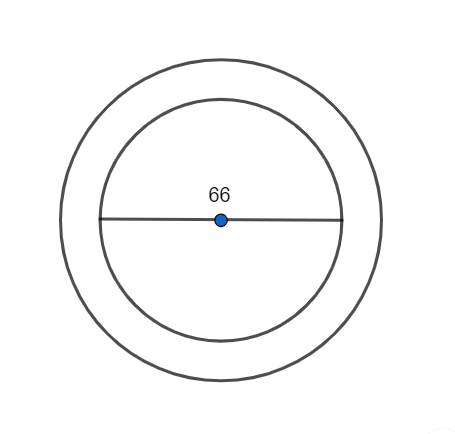
A circular flower bed is surrounded by a path 4 m wide. The diameter of the flower bed is 66 m. What is the area of this path? (Take \[\pi = 3.14\])

Answer 1

Hint: Find the radius of the inner circle and the radius of the outer circle. Find the area of the circles using the formula \[A = \pi {r^2}\]. Then, find the difference between the areas to find the area of the path.

Complete step-by-step answer:
A circle is a closed two-dimensional figure with no corners or edges. It has a fixed point called the center from which all the points in the circle are at equal distances. The distance from the center to any point on the circle is called the radius. The diameter is the line segment passing through the center of the circle and having endpoints on the circle.

The relations between diameter d and radius r is given as follows:
\[r = \dfrac{d}{2}..............(1)\]

The flower bed is circular and the diameter is given to be 66 m.
The radius of the flower bed can be calculated from formula (1) as follows:
\[{r_1} = \dfrac{{66}}{2}\]
\[{r_1} = 33m.............(2)\]

The area of a circle of radius r is given as follows:
\[A = \pi {r^2}............(3)\]
From equation (2) and formula (3), the area of the flower bed is given as follows:
\[{A_1} = 3.14 \times {(33)^2}\]
\[{A_1} = 3419.46{m^2}............(4)\]

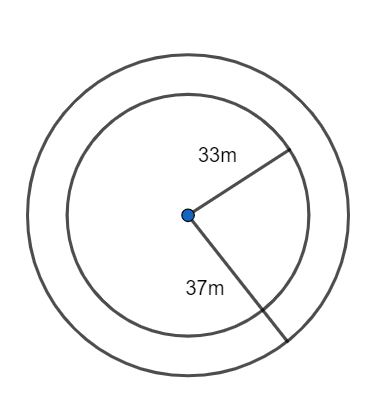
The radius of the bigger circle containing the path is the sum of 33 m and 4 m, that is, the width of the path.
\[{r_2} = 37m.............(5)\]
From equation (5) and formula (3), the area of the flower bed is given as follows:
\[{A_2} = 3.14 \times {(37)^2}\]
\[{A_2} = 4298.66{m^2}............(6)\]
From equations (4) and (6), the area of the path is given as follows:

From equation (2) and formula (3), the area of the flower bed is given as follows:
\[A = {A_2} - {A_1}\]
\[A = 4298.66 - 3419.46\]
\[A = 879.2{m^2}\]
Hence, the answer is 879.2 \[{m^2}\].

Note: Be careful when determining the radius of the outer circle, the width of the path is itself 4 m and hence, the radius should be added with 4 m and not the diameter.