Question

A circle with radius \[\left| a \right|\] and centre on y-axis slides along it and a variable line though \[\left( {a,0} \right)\] cuts the circle at points \[P\] and \[Q\]. The region in which the point of intersection of tangents to the circle at points \[P\] and \[Q\] lies is represented by
A. \[{y^2} \geqslant 4\left( {ax - {a^2}} \right)\]
B. \[{y^2} \leqslant 4\left( {ax - {a^2}} \right)\]
C. \[y \geqslant 4\left( {ax - {a^2}} \right)\]
D. \[y \leqslant 4\left( {ax - {a^2}} \right)\]

Answer 1

Hint: First of all, consider the centre of the circle as a variable on the y-axis and find the equation of the circle. Then find the equation of chord of contact at points \[P\] and \[Q\]. As the value of the y-coordinate of the centre of the circle is real, equate the value of discriminant to greater than or equal to zero.

Complete step-by-step answer:
Given radius of the circle is \[\left| a \right|\]
Let \[\left( {0,\alpha } \right)\] be the centre of the circle as the centre lies on the y-axis.
We know that the equation of the circle with centre \[\left( {h,k} \right)\] and radius \[r\] is given by \[{\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}\].
So, the given circle equation is given by
\[
  {\left( {x - 0} \right)^2} + {\left( {y - \alpha } \right)^2} = {\left( {\left| a \right|} \right)^2} \\
  {x^2} + {\left( {y - \alpha } \right)^2} = {a^2} \\
  {x^2} + {y^2} - 2\alpha y + {\alpha ^2} - {a^2} = 0 \\
  {x^2} + {y^2} - 2\alpha y + \left( {{\alpha ^2} - {a^2}} \right) = 0 \\
\]
Let \[R\left( {h,k} \right)\] be the point of intersection of the tangents to the circle at points \[P\] and \[Q\] as shown in the below figure:

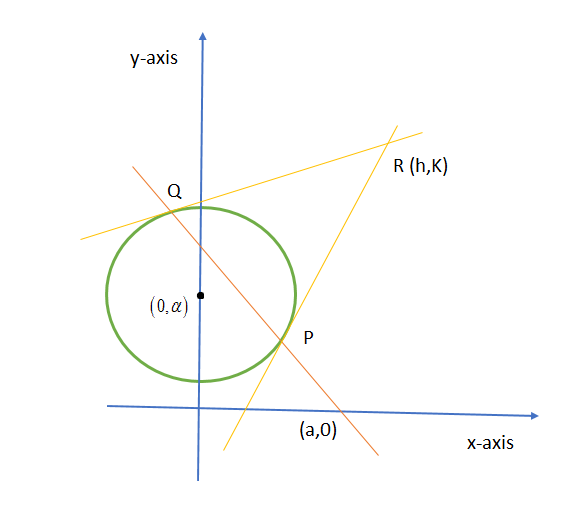
We know that the equation of chord of contact at \[\left( {{x_1},{y_1}} \right)\] to the circle \[{x^2} + {y^2} + 2gx + 2fy + c = 0\] is given by \[x{x_1} + y{y_1} + g\left( {x + {x_1}} \right) + f\left( {y + {y_1}} \right) + c = 0\].
So, the equation of chord of contact i.e., equation of PQ is given by
\[
  xh + yk + 0\left( {x + h} \right) + \left( { - \alpha } \right)\left( {y + k} \right) + \left( {{\alpha ^2} - {a^2}} \right) = 0 \\
  xh + yk - \alpha \left( {y + k} \right) + \left( {{\alpha ^2} - {a^2}} \right) = 0 \\
\]
But this equation is passing through \[\left( {a,0} \right)\]. So, this point should satisfy the equation PQ.
\[
  ah + \left( 0 \right)k - \alpha \left( {0 + k} \right) + \left( {{\alpha ^2} - {a^2}} \right) = 0 \\
  ah - \alpha k + {\alpha ^2} - {a^2} = 0 \\
  {\alpha ^2} - \alpha k + ah - {a^2} = 0 \\
\]
We know that for the equation \[a{x^2} + bx + c = 0\] if \[x\] is a real value then its discriminant must be greater than or equal to zero i.e., \[{b^2} - 4ac \geqslant 0\].
In the equation \[{\alpha ^2} - \alpha k + ah - {a^2} = 0\] as \[\alpha \] is a real since it is a variable and lies on y-axis its discriminant must be greater than equal to zero.
So, we have
\[
  {\left( { - k} \right)^2} - 4\left( 1 \right)\left( {ah - {a^2}} \right) \geqslant 0 \\
  {k^2} - 4\left( {ah - {a^2}} \right) \geqslant 0 \\
  {k^2} \geqslant 4\left( {ah - {a^2}} \right) \\
\]
As we have to find the coordinates of \[\left( {h,k} \right)\], we substitute \[h = x\] and \[k = y\], then we get
\[{y^2} \geqslant 4\left( {ax - {a^2}} \right)\]
Thus, the correct option is A. \[{y^2} \geqslant 4\left( {ax - {a^2}} \right)\]

Note: The chord joining the points of contact of the two tangents to a conic drawn from a given point, outside it, is called the chord of contact. For the equation \[a{x^2} + bx + c = 0\] if \[x\] is a real value then its discriminant must be greater than or equal to zero i.e., \[{b^2} - 4ac \geqslant 0\].