Answer
Verified496.5k+ views
Hint: Use the fact that if the circle touches both the coordinate axes, then distance between the centre of the circle and the points at which the circle touches the coordinate axes is equal and is equal to the radius of the circle.
Complete step-by-step answer:
We have a circle which touches both the coordinate axes at points \[\left( 3,0 \right)\] and \[\left( 0,-3 \right)\].
We want to find the centre of the circle.
Let’s assume that the centre of the circle is at any point \[\left( h,k \right)\].
We know that the distance between the centre of the circle and the points at which the circle touch the coordinate axes is equal and is equal to the radius of the circle.
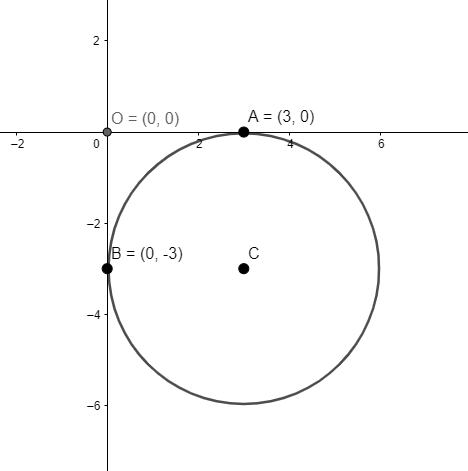
In the figure above, we observe that as lines \[AO\] and \[BC\] are parallel and are of equal length which is equal to the radius of the circle.
Thus, distance between \[C\left( h,k \right)\] and \[B\left( -0,-3 \right)\] is same as distance between \[A\left( 3,0 \right)\] and \[O\left( 0,0 \right)\] which is equal to the radius of the circle.
We know that distance between any two points of the form \[\left( a,b \right)\] and \[\left( c,d \right)\] is \[\sqrt{{{\left( a-c \right)}^{2}}+{{\left( b-d \right)}^{2}}}\].
Substituting \[a=0,b=3,c=0,d=0\] in the above equation, we get distance between \[A\left( 3,0 \right)\] and \[O\left( 0,0 \right)\] is \[\sqrt{{{\left( 0-0 \right)}^{2}}+{{\left( 3-0 \right)}^{2}}}=\sqrt{{{3}^{2}}}=3\] units which is the radius of the circle.
Substituting \[a=h,b=k,c=0,d=-3\] in the distance formula, we get \[\sqrt{{{\left( h-0 \right)}^{2}}+{{\left( k+3 \right)}^{2}}}=\sqrt{{{\left( h \right)}^{2}}+{{(k+3)}^{2}}}\] as the distance between points \[C\left( h,k \right)\] and \[B\left( 0,-3 \right)\].
We know that this distance is equal to the radius of the circle which is \[3\] units.
Substituting \[a=h,b=k,c=3,d=0\] in the distance formula, we get \[\sqrt{{{\left( h-3 \right)}^{2}}+{{\left( k+0 \right)}^{2}}}=\sqrt{{{\left( h-3 \right)}^{2}}+{{k}^{2}}}\] as the distance between points \[C\left( h,k \right)\] and \[A\left( 3,0 \right)\].
We know that this distance is equal to the radius of the circle which is \[3\] units.
Thus, we have \[\sqrt{{{\left( h \right)}^{2}}+{{(k+3)}^{2}}}=\sqrt{{{\left( h-3 \right)}^{2}}+{{k}^{2}}}=3\].
Solving first two equations by squaring them, we get \[{{h}^{2}}+{{k}^{2}}+9+6k={{h}^{2}}+{{k}^{2}}+9-6h\].
\[\Rightarrow k=-h\] \[...\left( 1 \right)\]
Substituting equation \[\left( 1 \right)\] in the equation \[\sqrt{{{\left( h-3 \right)}^{2}}+{{k}^{2}}}=3\], we get \[\sqrt{{{\left( h-3 \right)}^{2}}+{{\left( -h \right)}^{2}}}=3\].
Solving the equation by squaring on both sides, we get \[2{{h}^{2}}-6h=0\].
\[\Rightarrow 2h\left( h-3 \right)=0\]
Thus, we have \[h=3\] as we will reject \[h=0\] because it will give us origin which doesn’t lie in the circle.
So, we get \[k=-3\].
Thus, the centre of the circle is \[\left( h,k \right)=\left( 3,-3 \right)\].
Hence, the correct answer is \[\left( 3,-3 \right)\].
Answer is Option (a).
Note: It is necessary to draw the figure and observe that the distance between the centre of the circle and the points at which the circle touches the coordinate axes is equal and is equal to the radius of the circle.
Complete step-by-step answer:
We have a circle which touches both the coordinate axes at points \[\left( 3,0 \right)\] and \[\left( 0,-3 \right)\].
We want to find the centre of the circle.
Let’s assume that the centre of the circle is at any point \[\left( h,k \right)\].
We know that the distance between the centre of the circle and the points at which the circle touch the coordinate axes is equal and is equal to the radius of the circle.
In the figure above, we observe that as lines \[AO\] and \[BC\] are parallel and are of equal length which is equal to the radius of the circle.
Thus, distance between \[C\left( h,k \right)\] and \[B\left( -0,-3 \right)\] is same as distance between \[A\left( 3,0 \right)\] and \[O\left( 0,0 \right)\] which is equal to the radius of the circle.
We know that distance between any two points of the form \[\left( a,b \right)\] and \[\left( c,d \right)\] is \[\sqrt{{{\left( a-c \right)}^{2}}+{{\left( b-d \right)}^{2}}}\].
Substituting \[a=0,b=3,c=0,d=0\] in the above equation, we get distance between \[A\left( 3,0 \right)\] and \[O\left( 0,0 \right)\] is \[\sqrt{{{\left( 0-0 \right)}^{2}}+{{\left( 3-0 \right)}^{2}}}=\sqrt{{{3}^{2}}}=3\] units which is the radius of the circle.
Substituting \[a=h,b=k,c=0,d=-3\] in the distance formula, we get \[\sqrt{{{\left( h-0 \right)}^{2}}+{{\left( k+3 \right)}^{2}}}=\sqrt{{{\left( h \right)}^{2}}+{{(k+3)}^{2}}}\] as the distance between points \[C\left( h,k \right)\] and \[B\left( 0,-3 \right)\].
We know that this distance is equal to the radius of the circle which is \[3\] units.
Substituting \[a=h,b=k,c=3,d=0\] in the distance formula, we get \[\sqrt{{{\left( h-3 \right)}^{2}}+{{\left( k+0 \right)}^{2}}}=\sqrt{{{\left( h-3 \right)}^{2}}+{{k}^{2}}}\] as the distance between points \[C\left( h,k \right)\] and \[A\left( 3,0 \right)\].
We know that this distance is equal to the radius of the circle which is \[3\] units.
Thus, we have \[\sqrt{{{\left( h \right)}^{2}}+{{(k+3)}^{2}}}=\sqrt{{{\left( h-3 \right)}^{2}}+{{k}^{2}}}=3\].
Solving first two equations by squaring them, we get \[{{h}^{2}}+{{k}^{2}}+9+6k={{h}^{2}}+{{k}^{2}}+9-6h\].
\[\Rightarrow k=-h\] \[...\left( 1 \right)\]
Substituting equation \[\left( 1 \right)\] in the equation \[\sqrt{{{\left( h-3 \right)}^{2}}+{{k}^{2}}}=3\], we get \[\sqrt{{{\left( h-3 \right)}^{2}}+{{\left( -h \right)}^{2}}}=3\].
Solving the equation by squaring on both sides, we get \[2{{h}^{2}}-6h=0\].
\[\Rightarrow 2h\left( h-3 \right)=0\]
Thus, we have \[h=3\] as we will reject \[h=0\] because it will give us origin which doesn’t lie in the circle.
So, we get \[k=-3\].
Thus, the centre of the circle is \[\left( h,k \right)=\left( 3,-3 \right)\].
Hence, the correct answer is \[\left( 3,-3 \right)\].
Answer is Option (a).
Note: It is necessary to draw the figure and observe that the distance between the centre of the circle and the points at which the circle touches the coordinate axes is equal and is equal to the radius of the circle.