Question

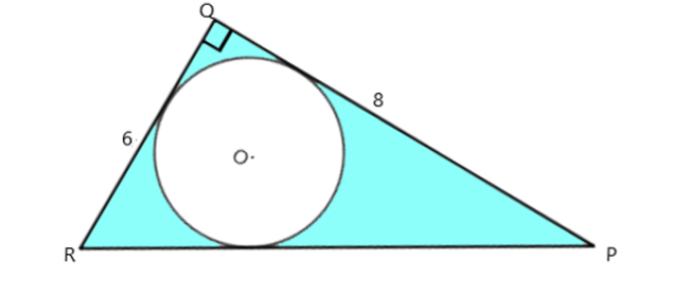
A circle is inscribed in $ \Delta PQR $ , where $ \angle Q = {90^ \circ },PR = 8cm $ and $ QR = 6cm $ . Find the area of the blue coloured regain as shown in the figure. ( Take $ \pi = 3.14 $ ).

Answer 1

Hint: As we can see in the above figure we have a right angled triangle, since one of its angles is $ {90^ \circ } $ . We have to find the area of the shaded region, so we can calculate it by the formula i.e. if we subtract the area of the circle from the area of the triangle, then we can find the area of the shaded region. We know the formula for the area of the triangle is $ \dfrac{1}{2} \times base \times height $ and the area of the circle is $ \pi {r^2} $ , where $ r $ is the radius of the circle.

Complete step by step solution:
We need to first understand the requirement of the question which is the shaded area or the left area inside the triangle apart from the circle.
Since $ \Delta PQR $ , is a right angled triangle so we can find the hypotenuse i.e. PR . We know that $ h = \sqrt {{b^2} + {p^2}} $ , where we have to find $ h $ i.e. hypotenuse (PR) , $ b $ is the base i.e. $ QR = 8 $ and $ p $ is the perpendicular ( PQ) $ = 6 $ cm.
So by applying the formula and substituting the values we have
$ PR = \sqrt {{8^2} + {6^2}} $ .
We will solve it now i.e. $ PR = \sqrt {64 + 36} = \sqrt {100} $.
It gives us the value $ 10 $ cm.
Now the area of the triangle is $ \dfrac{1}{2} \times base \times height $ , by putting the value we have $ Area = \dfrac{1}{2} \times 8 \times 6 $ .
The area of the triangle is $ 24c{m^2} $ .
Now we have to find the area of the circle, for this we have to find the radius.
So let us join a line from the centre O to the line PR at A , so we have $ OA = r $ i.e. radius of the circle. Let us draw the diagram of the radius too:

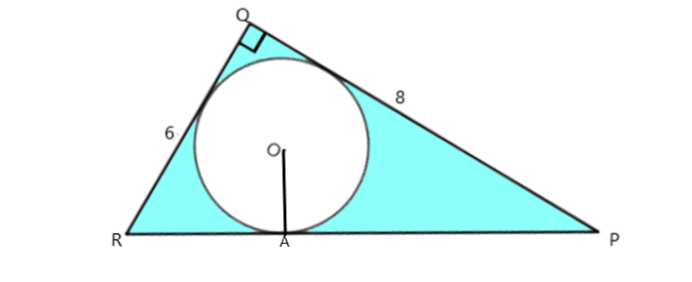
We should know the relation by which we can find the radius which is $ \dfrac{{areaof\,triangle}}{{perimeter\,of\,triangle}} = \dfrac{1}{2}radius $ .
We have the area of the triangle and the perimeter is the sum of all the sides of the triangle. So here we have perimeter : $ 8 + 6 + 10 = 24cm $ .
Now we can calculate the radius by putting the values i.e.
$ \dfrac{{24}}{{24}} = \dfrac{1}{2} \times r $ .
On simplifying we have $ 1 = \dfrac{1}{2} \times r $ .
So by cross multiplication we have $ r = 2cm $ .
We can find the area of the circle i.e.
$ \pi {r^2} = 3.14 \times 2 \times 2 $ . It gives us an area of circle $ = 12.56 $ .
Now we can find the area of the shaded region $ = $ area of triangle $ - $ area of circle.
By substituting the values we can write that the area of the shaded region is
$ 24 - 12.56 = 11.43c{m^2} $ .
Hence the required answer is $ 11.43c{m^2} $ .
So, the correct answer is “ $ 11.43c{m^2} $ ”.

Note: We should always be careful what the question is asking . Based on the requirement and by observing all the necessary information that is already available in the question we gather the information and then we solve the problem and then verify the answer by putting the value in the problem and see whether we get the same answer or not. We should know that if the above given triangle will not be the right angled triangle, then we can also calculate the area by the Heron’s formula which is $ Area = \sqrt {s(s - a)(s - b)(s - c)} $ , where $ s = \dfrac{{a + b + c}}{2} $ and $ a,b,c $ are all the three sides of a triangle.