Question

A circle is inscribed in a triangle whose sides are 8 cm, 15 cm, and 17 cm, then the radius of the circle is
(a) 3 cm
(b) 4 cm
(c) 5 cm
(d) None of these

Answer 1

Hint: In this question, first we will prove that the triangle is a right angled triangle. Then, find the area of the right-angled triangle. After that, we will draw the line segments with the centre of the circle and all corners of the triangle. Now, we have to evaluate the area of all 3 triangles. Now, on comparing both the areas, we will get the radius of the circle.

Complete step-by-step answer:

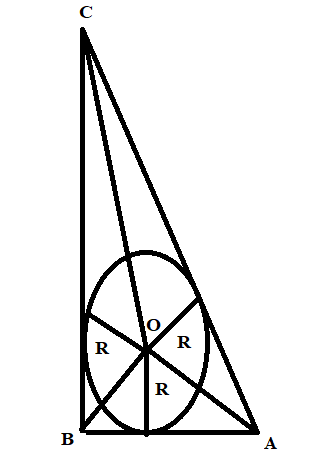
Let, the \[\Delta ABC\] have the dimensions AB = 8cm, BC = 15cm and AC = 17cm.
Now, we have to prove that ABC is a right-angled triangle. So, by using Pythagoras theorem $\left( {{a}^{2}}+{{b}^{2}}={{c}^{2}} \right)$ :
$\begin{align}
  & A{{B}^{2}}+B{{C}^{2}}={{8}^{2}}+{{15}^{2}}=64+225=289 \\
 & A{{C}^{2}}={{17}^{2}}=289 \\
\end{align}$
Hence, it satisfies Pythagoras theorem. So, the ABC is a right-angled triangle.
Area of $\Delta ABC=\dfrac{1}{2}\times Base\times Height$
Base = 8 cm and height = 15 cm.
Area of $\Delta ABC=\dfrac{1}{2}\times 8\times 15=60c{{m}^{2}}...(1)$
Let, R be the radius of the circle, whose centre is O.
Now, calculate area of all 3 triangles in the figure in terms of radius of the circle R,
= area of $\Delta AOB$+ area of $\Delta BOC$+ area of $\Delta COA$
$\begin{align}
  & =\left[ \dfrac{1}{2}\times AB\times R \right]+\left[ \dfrac{1}{2}\times BC\times R \right]+\left[ \dfrac{1}{2}\times AC\times R \right] \\
 & =\dfrac{1}{2}\times R\times \left[ 8+15+17 \right]=\dfrac{1}{2}\times R\times 40 \\
 & =20R...(2) \\
\end{align}$
The area obtained in equation (2) is also the area of the right-angled triangle because the sum of the area of all 3 triangles is the area of the right-angled triangle.
From equation (1) and equation (2), we get
$\begin{align}
  & 20\times R=60 \\
 & R=3cm \\
\end{align}$
Hence, the radius of the circle is 3 cm.
Therefore, option (a) is correct.

Note: The key concept for solving this problem is the segregation of the whole area into three parts. By separating the area into three triangles we easily evaluated the radius of the circle. This concept is very useful in solving complex problems.