Question

A circle is divided into 12 equal parts. The number of degrees in each arc is?

Answer 1

Hint: Circle- the circle is a geometrical shape that is made up of an infinite number of points in a plane that are located at a fixed distance from a point called as the center of the circle.

Arc of a circle - An arc of a circle is a "portion" of the circumference of the circle. The length of
an arc is simply the length of its "portion" of the circumference.

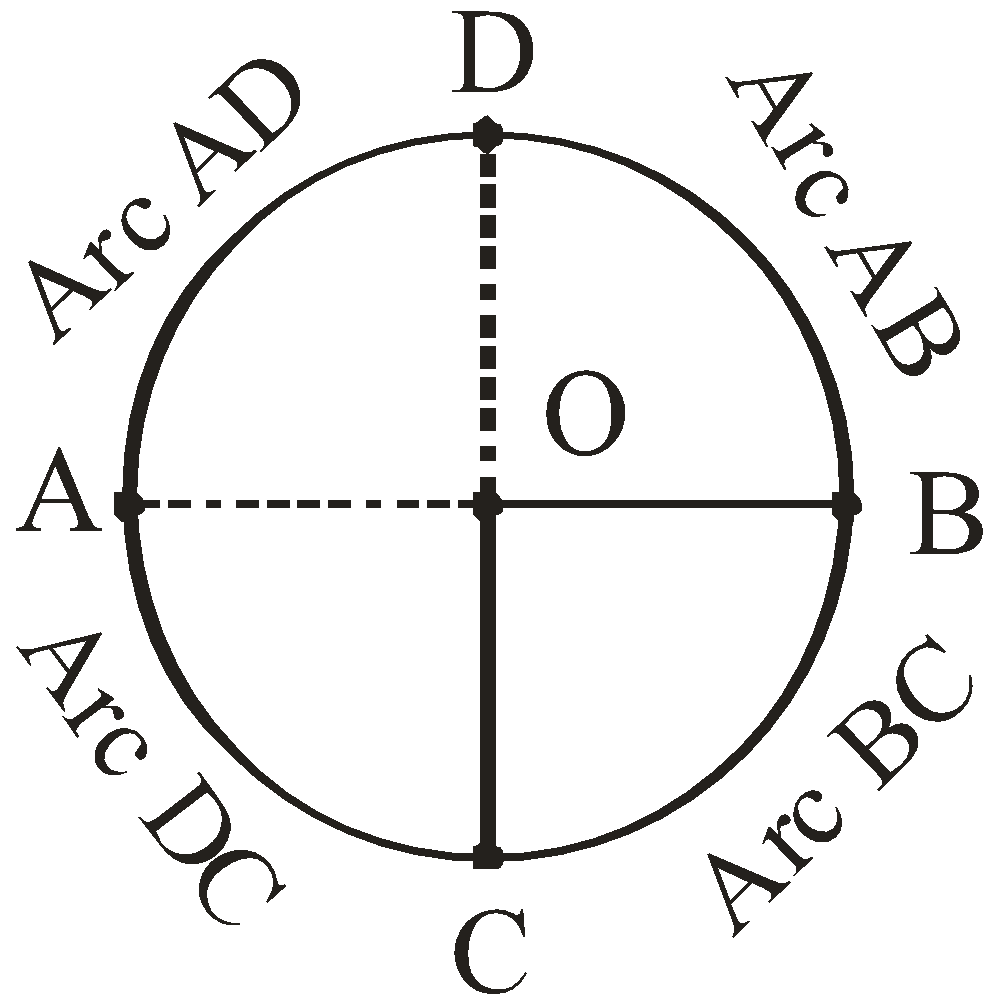
In the below diagram :
O is the center of the circle.
And here portion on circle AB is arc of a circle.
If we take portion other than arc AB then that arc will be a major arc.

Every circle is an angle of \[360^\circ \] and if we join the two ends of an arc to the center O of the circle
then it will divide the circle in two or more than two angles depends on the number of arcs.
Like -
If we make 4 equal arcs then, angle \[360^\circ \] will also divided in 4 parts and one part will be equal to,
$\dfrac{{360^\circ }}{4} = 90^\circ $
We can see this in below diagram.

So we can use the formula,
Angle subtended by equal arcs $ = \dfrac{{360^\circ }}{{Number\,of\,arcs}}$
Let’s solve the given question-
Complete step by step answer:
We need to find out angles by 12 equal arcs.
For this first, we will understand the question with the help of a diagram.
Let O be the center of a circle and arc AB, arc BC ,arc CD , arc DE , arc EF, arc FG, arc GH, arc HI, arc
IJ, arc JK, arc KL and arc LA are 12 equal arcs of this circle. They divide this circle in 12 equal angles.

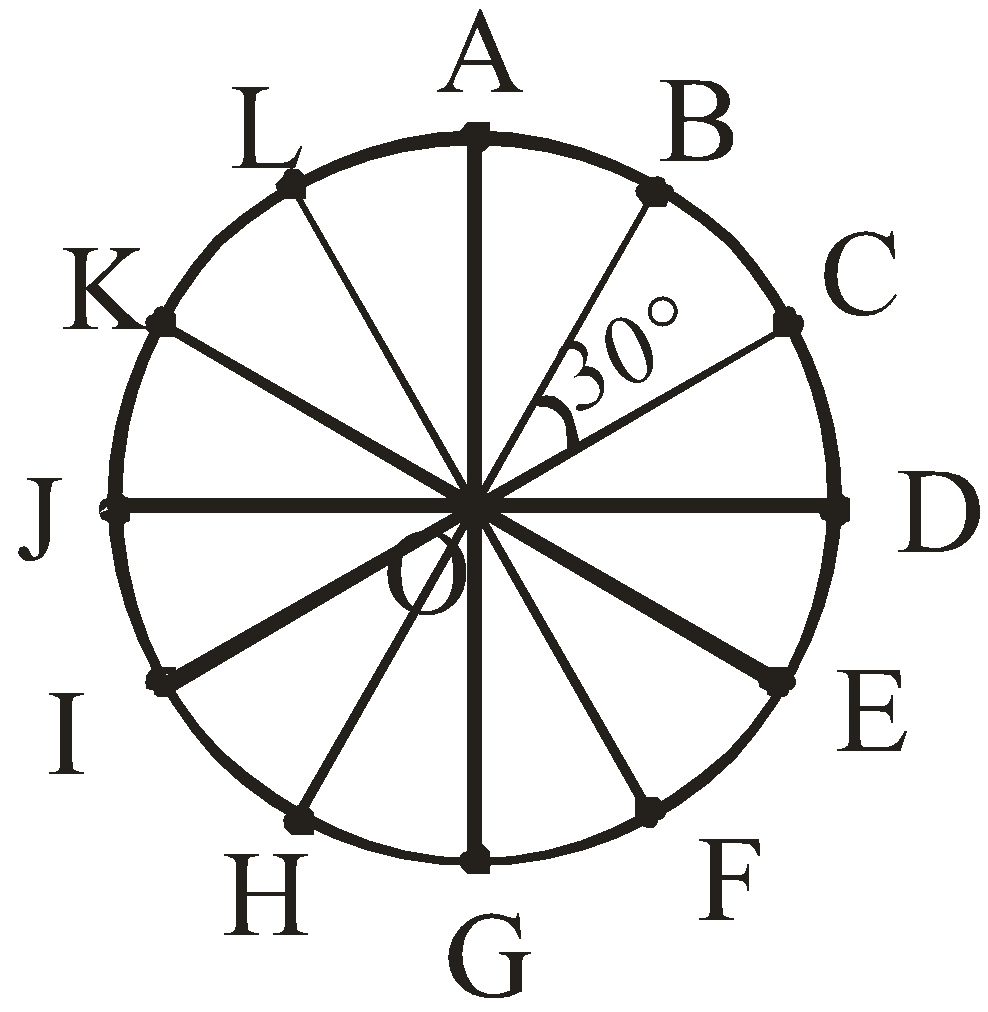
As we know that ,
Angle made by equal arcs $ = \dfrac{{360^\circ }}{{Number\,of\,arcs}}$
$\dfrac{{360^\circ }}{{12}} = 30^\circ $
Therefore,
If a circle is divided into 12 equal parts then the number of degrees in each arc is $30^\circ $.

Note:
 An arc could be a minor arc, a semicircle or a major arc.
A semicircle is an arc that is half a circle.
A minor arc is an arc that is smaller than a semicircle.
A major arc is an arc that is larger than a semicircle.

We can also find out the length of the arc if we know the angle subtended by it on the center of the circle and radius of that circle.
Like, if the angle formed by the arc is $\theta $.
And the radius is r.
Then,
Length of arc $ = \dfrac{\theta }{{360^\circ }} \times 2\pi r$
Where \[360^\circ \] is an angle formed by the whole circle
And \[2\pi r\] is the total length of the circle i.e. circumference of a circle.