Question

A circle has a sector with area \[33\pi \] and central angle of \[\dfrac{{11}}{6}\pi \] radians. What is the area of the following circle? Either enter an exact answer in terms of \[\pi \] or use 3.14 for \[\pi \].

Answer 1

Hint: We are provided with an area of a sector in a circle and central angle in the circle and we are told to find the area of the circle. For that, we have to compare the given area of the sector with the formula of the area and by substituting the known values we get the required area of a circle.

Formula used:
The area of a sector is given by,
 \[{\text{The area of the sector}} = \dfrac{{{\text{Central angle}}}}{{2\pi }} \times {\text{ Area of the circle}}\]

Complete step by step solution:

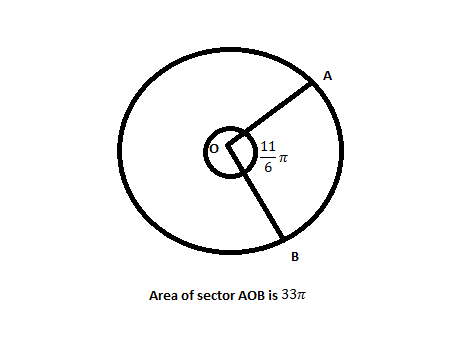
Here we are provided with the area of sector in a circle and the central angle in radians. We should find the area of the circle in which the sector is found.
For finding the area of the circle we are going to use the formula of area of sectors. The area of sectors is given by the following formula,
The area of sectors\[ = \dfrac{{{\text{Central angle}}}}{{2\pi }} \times {\text{ Area of the circle}}\]
We are given that area of sector is \[33\pi \],
Also let us consider the area of circle as “A”.
Also central angle is given as \[\dfrac{{11}}{6}\pi \] radians.
By substituting the values in the formula of area of sectors we get,
\[{\rm{33}}\pi {\rm{ = }}\dfrac{{\dfrac{{11}}{6}\pi }}{{2\pi }} \times A\]
Let us cancel the terms in the fraction we get,
\[33\pi = \dfrac{{11}}{{12}}A\]
Let us multiply by\[\dfrac{{12}}{{11}}\]on both sides of the above equation we get,
\[\dfrac{{12}}{{11}} \times 33\pi = A\]
By cancelling the terms and rearranging the above equation we get,
\[A = 36\pi \]

$\therefore$ Hence we have found that the area of the circle with area of sector \[33\pi \] and central angle \[\dfrac{{11}}{6}\pi \] radians is \[36\pi {\rm{ uni}}{{\rm{t}}^2}\].

Note:
 Here we are dividing by \[2\pi \] in the area of sectors this is done because the total angle in a circle is \[2\pi \] radians. If the central angles is given in degree then we divide by \[360^\circ \] in the area of sectors formula. Hence we should be careful in choosing the correct formula.