Question

A chord PQ of a circle with radius 15 cm subtends an angle of 600 with the centre of the circle. Find the area of the minor as well as the major segment.

Answer 1

Hint-In this question, we use the concept of sector and segment of a circle. To calculate the area of segments so first we have to find the area of the sector. Area of sector \[ = \dfrac{{\pi {r^2}\theta }}{{{{360}^0}}}\] ,where $\theta $ is the angle subtended by chord at the center of circle.

Complete step-by-step solution -

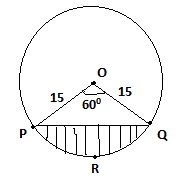
Consider a circle of radius (r) 15cm and have a chord PQ subtend an angle 600 at the center of circle O.
Now, area of minor segment= (area of sector OPRQ)-(area of triangle OPQ)
Area of sector OPRQ \[ = \dfrac{{\pi {r^2}\theta }}{{{{360}^0}}}\] , where $\theta = {60^0}$ and radius of circle, $r = 15cm$
$
   \Rightarrow \dfrac{{\pi \times {{\left( {15} \right)}^2} \times 60}}{{360}} \\
   \Rightarrow \dfrac{{\pi \times 15 \times 15}}{6} \\
$
Put value of $\pi = 3.14$ ,
$
   \Rightarrow \dfrac{{3.14 \times 15 \times 15}}{6} \\
   \Rightarrow 117.75c{m^2} \\
$
Area of sector OPRQ= 117.75cm2.
Now, we have to find area of $\vartriangle OPQ$ .
We can see the $\angle OPQ = {60^0}$ and OP=OQ=r. So, $\angle OPQ = \angle OQP$
In $\vartriangle OPQ$, the sum of all angles of the triangle is 1800.
\[
   \Rightarrow \angle OPQ + \angle OPQ + \angle OQP = {180^0} \\
   \Rightarrow {60^0} + 2\angle OPQ = {180^0} \\
   \Rightarrow 2\angle OPQ = {120^0} \\
   \Rightarrow \angle OPQ = {60^0} \\
\]
$\angle OPQ = \angle OQP = {60^0}$
So, the $\vartriangle OPQ$ is an equilateral triangle and we know the area of the equilateral triangle is $\dfrac{{\sqrt 3 }}{4}{a^2}$ , where a is the side of the equilateral triangle.
$
  {\text{Area of }}\vartriangle OPQ = \dfrac{{\sqrt 3 }}{4}{r^2} \\
   \Rightarrow \dfrac{{\sqrt 3 }}{4} \times 15 \times 15 \\
 $
Use value of $\sqrt 3 = 1.732$
$
   \Rightarrow \dfrac{{1.732}}{4} \times 15 \times 15 \\
   \Rightarrow 97.42c{m^2} \\
 $
\[
  {\text{area of minor segment}} = {\text{ }}\left( {{\text{area of sector OPRQ}}} \right) - \left( {{\text{area of triangle OPQ}}} \right) \\
   \Rightarrow {\text{area of minor segment}} = 117.75 - 97.42 \\
   \Rightarrow {\text{area of minor segment}} = 20.33c{m^2} \\
 \]
Now, area of major segment = area of circle –area of minor segment
\[
  {\text{area of major segment}} = \pi {r^2} - 20.33 \\
   \Rightarrow {\text{area of major segment}} = 3.14 \times 15 \times 15 - 20.33 \\
   \Rightarrow {\text{area of major segment}} = 706.5 - 20.33 \\
   \Rightarrow {\text{area of major segment}} = 686.17 \\
 \]
So, the area of minor and major segment is $20.33cm^2$ and $686.17cm^2$ respectively.

Note-In such types of questions sometimes we face problems to find the area of the triangle. Like in the above question we can easily see that it is an equilateral triangle but it’s not possible every time. So, the correct way to find area of triangle, first draw the perpendicular from center of circle to chord and then use of trigonometric ratio find the length of perpendicular and chord then use area of triangle is $\dfrac{1}{2} \times \left( {{\text{Base}}} \right) \times \left( {{\text{Height}}} \right)$ .