Question

A chord PQ of a circle of radius 10cm subtends an angle of \[{{60}^{\circ }}\] at the center of the circle. Find the area of major and minor segments of the circle.

Answer 1

Hint: The first step we will do is construct the figure as per the details given in the question. To solve this question we will use the area of the sector of the circle. Area of a sector of the circle when the angle is \[\theta \] and radius is r is,
Area = \[\dfrac{\theta }{{{360}^{\circ }}}\times \pi {{\left( r \right)}^{2}}\]
Also, we will need one more concept that a full circle angle measures angle \[{{360}^{\circ }}\].

Complete step-by-step solution:
Let us first do the necessary construction to solve this question.
Let given below be the circle of center O and radius OP = 10cm.
Also, \[\angle POQ={{60}^{\circ }}\] this is given,

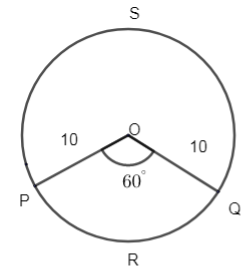
Clearly, OP and OQ are both radii.
So, $OP = OQ = 10cm$.
Consider a point R and S on the circumference of the circle as shown in the figure.
Then POQR is the minor segment and POQS is the major segment.
Form line PQ.

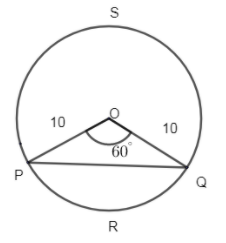
Now we will finally compute the area of minor and major segment of the circle.
The area of the segment of the circle where \[\theta \] is the angle and radius is r is given by,
Area = \[\dfrac{\theta }{{{360}^{\circ }}}\times \pi {{\left( r \right)}^{2}}\]
Now here for area of minor segment POQR we have, \[\theta ={{60}^{\circ }}\] and r = 10.
Then using the formula of area of the sector we have,
Area of sector POQR = \[\dfrac{\theta }{{{360}^{\circ }}}\times \pi {{\left( r \right)}^{2}}\]
Substituting \[\theta ={{60}^{\circ }}\] and r = 10.
\[\Rightarrow \] Area of minor segment POQR = \[\dfrac{{{60}^{\circ }}}{{{360}^{\circ }}}\times \pi \times {{\left( 10 \right)}^{2}}\].
Using \[\pi =3.14\] we get,
\[\Rightarrow \] Area of minor segment $POQR = \dfrac{1}{6}\times 3.14\times 100 $.
\[\Rightarrow \] Area of minor segment $POQR = 52.333 cm^2$.
Now for major segment POQS, we have to compute the angle.
Full circle angle is \[{{360}^{\circ }}\].
Then as \[\angle O=\angle POQ+\angle POQ\] (S side angle)
\[\Rightarrow \angle POQ\] (S side) = \[{{360}^{\circ }}-{{60}^{\circ }}\]
\[\Rightarrow \angle POQ\] (S side) = \[{{300}^{\circ }}\]
Then we have,
 

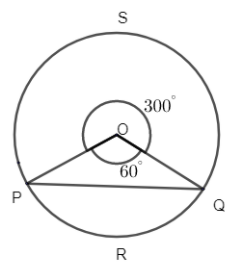
Then area, \[\theta ={{300}^{\circ }}\] of sector POQS and r = 10.
Then area of sector major POQS = \[\dfrac{{{300}^{\circ }}}{{{360}^{\circ }}}\times \pi \times {{\left( 10 \right)}^{2}}\]
Put, \[\pi =3.14\].
\[\Rightarrow \] Area of major segment $POQS = 0.83333 \times 3.14 \times 100$
\[\Rightarrow \] Area of major segment $POQS = 261.666 {{cm}^{2}}$.
Therefore area of minor segment = 52.333 \[c{{m}^{2}}\] and area of major segment = 261.666 \[c{{m}^{2}}\]

Note: The possibility of error in this question can be the point where we have to identify segments of the circle. The major segment of the circle is one that has a bigger angle at the center and the minor segment is one having a smaller angle at the center. Here the bigger angle is \[{{300}^{\circ }}\], so the major segment is POQS and the smaller angle is \[{{60}^{\circ }}\]. So the minor segment is POQR.