Question

A chord PQ is drawn inside the circle C1 of radius of 5 cm. Length of chord PQ is 8 cm. Tangents to the circle C1 are drawn from P and Q, these tangents intersect at point T. Find the length PT.

Answer 1

Hint: This question can be solved using some properties of a circle and its tangent and triangles.

Complete step-by-step answer:
Following properties will be useful in this question.
1. Tangent to the circle at any point is always perpendicular to the radius through that point.

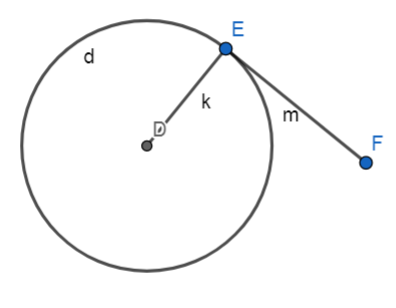
   ∠DEF = 90°
2. Perpendicular from centre of circle to the chord bisects the chord.

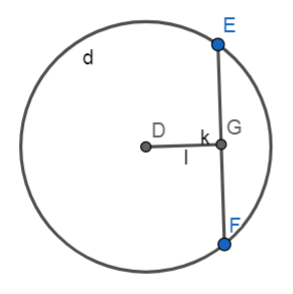
If DG ⊥ EF then EG = GF.
3. If two triangles are similar then the ratio of their corresponding sides are equal.

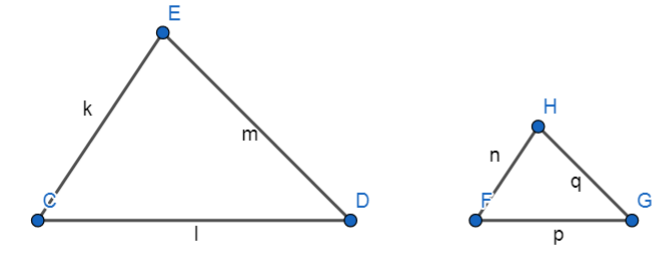
If ∆CDE ~ ∆FGH then $\dfrac{k}{n}=\dfrac{l}{p}=\dfrac{m}{q}$

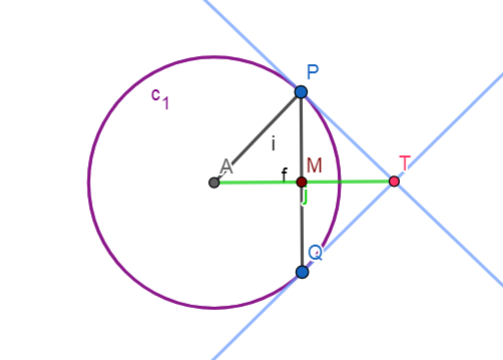
                                         Figure 1
In the figure above AP is the radius. PQ is a chord inside the circle C1. Radius of the circle is 5 cm. Length of chord PQ is 8 cm. Draw AM ⊥ PQ .
We know that, perpendicular to a chord of circle from the centre of circle bisects the chord.

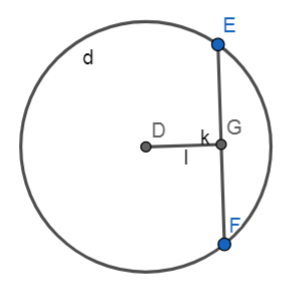
If DG ⊥ EF then EG = GF
Applying this concept in figure 1 we see that,
PM = MQ
But PM + MQ = PQ = 8 (given)
So PM = MQ = $\dfrac{8}{2}$ = 4 cm
Now in right triangle AMP, we have
AP = 5 (given)
PM = 4
Applying Pythagorean Theorem in triangle AMP we get
AP2 = AM2 + MP2
⇒ 52 = AM2 + 42
⇒ 25 = AM2 + 16
⇒ AM2 = 25 – 16 = 9
$\Rightarrow AM=\sqrt{9}=3$
We know that tangent to the circle at any point is perpendicular to radius through that point.

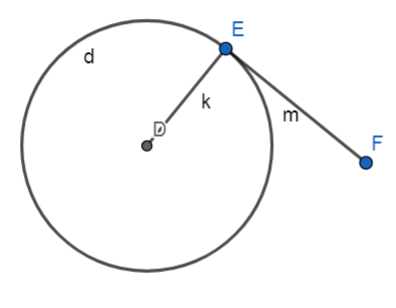
DE ⊥ EF
So applying this concept in figure 1 we get
∠APT = 90°.
Now in triangle APT and triangle APM,
∠APT = ∠AMP
∠PAT = ∠PAM
So combining both we conclude that ∆PAT ~ ∆MAP.
When two triangles are similar then the ratio of their corresponding sides is equal.
 

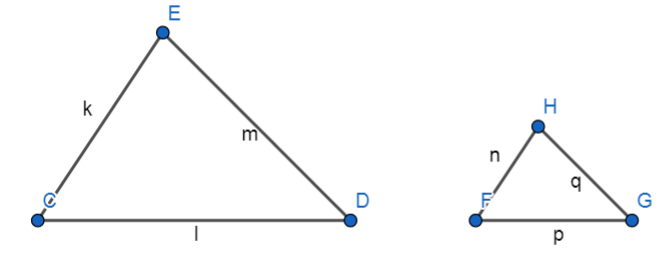
If ∆CDE ~ ∆FGH then $\dfrac{k}{n}=\dfrac{l}{p}=\dfrac{m}{q}$
Applying this concept in ∆PAT and ∆MAP we get
$\dfrac{PA}{MA}=\dfrac{PT}{MP}$
Putting the values of PA, MA, MP we get the value of PT as
$\begin{align}
  & \dfrac{5}{3}=\dfrac{PT}{4} \\
 & \Rightarrow PT=\dfrac{20}{3} \\
\end{align}$
Hence the length of PT is $\dfrac{20}{3}$ cm.

Note: Draw a diagram for better understanding of the question. One can make a mistake in writing the ratio of corresponding sides of similar triangles. Care must be taken while naming and referring to parts of the triangles as otherwise, the chances of error become very high.