Question

A chord of the circle \[{{x}^{2}}+{{y}^{2}}-4x-6y=0\] passing through the origin subtends an angle \[{{\tan }^{-1}}\left( \dfrac{7}{4} \right)\] at the point where the circle meets the positive y-axis. The equation of the chord is
(A) \[2x+3y=0\]
(B) \[x+2y=0\]
(C) \[x-2y=0\]
(D) \[2x-3y=0\]

Answer 1

Hint: Assume that the equation of the chord OP is \[y=mx\] , \[\angle OBP=\theta \] , and \[\angle GOY=\alpha \] . Now, get the coordinates of the points where the circle is intersecting the y-axis by putting \[x=0\] in the equation of the circle. The points are O (0,0) and B (0,6). Using, the equation of the circle, get the coordinate of its center C. Calculate the slope of the line joining the origin O and the center of the circle using the formula, \[Slope=\dfrac{{{x}_{2}}-{{x}_{1}}}{{{y}_{2}}-{{y}_{1}}}\] . Now, draw a line tangent XY to the circle. We know the property that the line drawn from the center is perpendicular to the tangent of the circle. We also know the property that the product of the slopes of two perpendicular lines is -1. Now, get the slope of the tangent to the circle. It is given that the chord subtends an angle \[{{\tan }^{-1}}\left( \dfrac{7}{4} \right)\] at the point where the circle meets the positive y-axis. So, \[\angle OBP=\theta ={{\tan }^{-1}}\left( \dfrac{7}{4} \right)\] . We know the property that the angles in the alternate segments are equal to each other. Using this property we can say that the \[\angle OBP\] and \[\angle POY\] are equal to each other. So, \[\angle POY=\theta ={{\tan }^{-1}}\left( \dfrac{7}{4} \right)\Rightarrow \tan \angle POY=\tan \theta =\dfrac{7}{4}\] . G is the point where the circle meets the x-axis. Now, using the slope of the tangent XY, get the tangent of the angle \[\angle GOY\] using the relation, \[\tan \angle GOY=-\tan \angle GOX\] . The slope of the chord OP is the tangent of the angle \[\angle POG\] . We have \[\angle POY-\angle GOY=\theta -\alpha \] . Now, use the formula, \[\tan \left( A-B \right)=\dfrac{\tan A-\tan B}{1+\tan A\tan B}\] and get the value of \[\tan \angle POY\] . We know that the slope of a line is the tangent of the angle measured from the x-axis in the anticlockwise direction. The equation of the chord is \[y=mx\] , where m is the slope of the line OP. Now, get the equation of the chord OP.

Complete step by step answer:
According to the question, it is given that the chord of the circle \[{{x}^{2}}+{{y}^{2}}-4x-6y=0\] is passing through the origin subtends an angle \[{{\tan }^{-1}}\left( \dfrac{7}{4} \right)\] at the point where the circle meets the positive y-axis.
Let us assume that the equation of the chord is \[y=mx+c\] .
Since the chord is passing through the origin so, we can say that the value of the y-intercept of the chord is equal to zero.
Now, the equation of the chord of the circle is \[y=mx\] …………………………..(1)
The equation of the circle is \[{{x}^{2}}+{{y}^{2}}-4x-6y=0\] …………………………………(2)
The center of the circle \[{{x}^{2}}+{{y}^{2}}-4x-6y\]=0 \Rightarrow \[\left( -\left( \dfrac{-4}{2} \right),-\left( \dfrac{-6}{2} \right) \right)=\left( 2,3 \right)\] ………………………………..(3)
We are given that the circle is also meeting the positive y-axis. The points where the circle is meeting the y-axis has the value of the x-coordinate equal to zero.
Now, on putting \[x=0\] in equation (2), we get
\[\begin{align}
  & \Rightarrow {{x}^{2}}+{{y}^{2}}-4x-6y=0 \\
 & \Rightarrow {{0}^{2}}+{{y}^{2}}-4\left( 0 \right)-6y=0 \\
 & \Rightarrow {{y}^{2}}-6y=0 \\
 & \Rightarrow y\left( y-6 \right)=0 \\
\end{align}\]
So, \[y=0\] or \[y=6\] .
The coordinate of the points where the circle is meeting the y-axis is \[\left( 0,0 \right)\] and \[\left( 0,6 \right)\] .

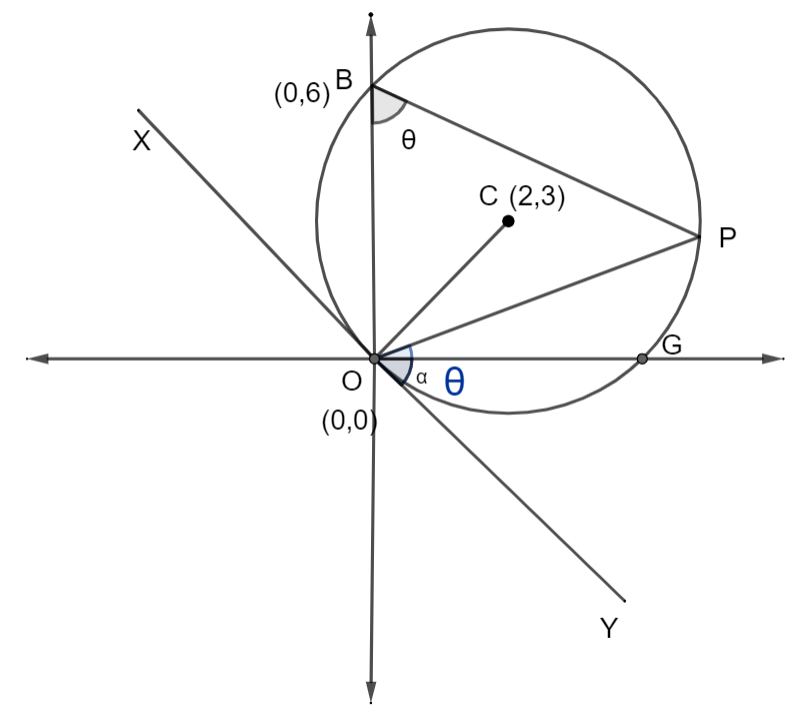
The slope of the line OC \[=\dfrac{{{x}_{2}}-{{x}_{1}}}{{{y}_{2}}-{{y}_{1}}}=\dfrac{3-0}{2-0}=\dfrac{3}{2}\] …………………………………….(4)
The line XY is tangent to the given circle.
We know the property that the line drawn from the center is perpendicular to the tangent of the circle.
Using this property, we can say that the line OC and XY are intersecting at \[90{}^\circ \] .
We also know the property that the product of the slopes of two perpendicular lines is -1.
Since the lines OC and XY are perpendicular so, the product of their slopes is equal to -1.
\[\text{Slope of the line OC }\!\!\times\!\!\text{ Slope of the line XY=}-1\] ………………………………………(5)
From equation (4), we have the slope of the line OC.
Now, from equation (4) and equation (5), we get
\[\begin{align}
  & \Rightarrow \text{Slope of the line OC }\!\!\times\!\!\text{ Slope of the line XY=}-1 \\
 & \Rightarrow \dfrac{3}{2}\,\text{ }\!\!\times\!\!\text{ }\left( \text{Slope of the line XY} \right)\text{=}-1 \\
 & \Rightarrow \text{Slope of the line XY}=\dfrac{-2}{3} \\
\end{align}\]
The slope of the line XY = \[\tan \angle GOX=\dfrac{-2}{3}\] …………………………………..(6)
We know the property that the angles in the alternate segments are equal to each other.
Using this property we can say that the \[\angle OBP\] and \[\angle POY\] are equal to each other.
So, \[\angle OBP=\angle POY\] ……………………………………(7)
It is given that the chord subtends an angle \[{{\tan }^{-1}}\left( \dfrac{7}{4} \right)\] at the point where the circle meets the positive y-axis. So,
\[\angle OBP=\theta ={{\tan }^{-1}}\left( \dfrac{7}{4} \right)\] ……………………………………..(8)
From equation (7) and equation (8), we have
\[\angle OBP=\angle POY={{\tan }^{-1}}\left( \dfrac{7}{4} \right)\] ………………………………………(9)
Now, on solving equation (8), we get
\[\Rightarrow \theta ={{\tan }^{-1}}\left( \dfrac{7}{4} \right)\]
\[\Rightarrow \tan \theta =\dfrac{7}{4}\] ……………………………….(10)
From equation (6), we have the slope of the line XY and we know that the slope of a line is the tangent of the angle measured from the x-axis in the anticlockwise direction. The tangent of the angle measured from the x-axis in the clockwise direction is negative of the tangent of the angle measured from the x-axis in the anticlockwise direction. So,
\[\tan \angle GOY=-\tan \angle GOX\] …………………………………………………(11)
Now, from equation (6) and equation (11), we have
\[\tan \angle GOY=\tan \alpha =-\left( \dfrac{-2}{3} \right)=\dfrac{2}{3}\] ……………………………………..(12)
From, the figure we can say that,
\[\angle POG=\angle POY-\angle GOY=\theta -\alpha \]
\[\tan \angle POG=\tan \left( \theta -\alpha \right)\] ………………………………………(13)
We know the formula, \[\tan \left( A-B \right)=\dfrac{\tan A-\tan B}{1+\tan A\tan B}\] ……………………….(14)
Now, from equation (13) and equation (14), we get
\[\Rightarrow \tan \angle POG=\tan \left( \theta -\alpha \right)\]
\[\Rightarrow \tan \angle POG=\dfrac{\tan \theta -\tan \alpha }{1+\tan \theta \tan \alpha }\] ……………………………………..(15)
Putting the value of \[\tan \theta \] from equation (10) and \[\tan \alpha \]from equation (12) in equation (15), we get
\[\begin{align}
  & \Rightarrow \tan \angle POG=\dfrac{\dfrac{7}{4}-\dfrac{2}{3}}{1+\left( \dfrac{7}{4} \right)\left( \dfrac{2}{3} \right)} \\
 & \Rightarrow \tan \angle POG=\dfrac{\dfrac{21-8}{12}}{1+\dfrac{14}{12}} \\
 & \Rightarrow \tan \angle POG=\dfrac{\dfrac{21-8}{12}}{\dfrac{12+14}{12}} \\
 & \Rightarrow \tan \angle POG=\dfrac{\dfrac{13}{12}}{\dfrac{26}{12}} \\
 & \Rightarrow \tan \angle POG=\dfrac{13}{26} \\
 & \Rightarrow \tan \angle POG=\dfrac{1}{2} \\
\end{align}\]
We know that the slope of a line is the tangent of the angle measured from the x-axis in the anticlockwise direction.
Therefore, the slope of the chord OP is \[\dfrac{1}{2}\] ………………………………….(16)
From equation (1), we have the equation of the chord OP.
The equation of the chord is \[y=mx\] , where m is the slope of the line OP ……………………………..(17)
Now, from equation (16) and equation (17), we get
\[\begin{align}
  & y=\dfrac{1}{2}x \\
 & \Rightarrow 2y=x \\
\end{align}\]
\[\Rightarrow x-2y=0\] ……………………………………(18)
Therefore, the equation of the chord OP is \[x-2y=0\] .

So, the correct answer is “Option C”.

Note: In this question, the main point that we have to keep in mind is that the slope of a line is the tangent of the angle measured from the x-axis in the anticlockwise direction. The tangent of the angle for the line measured from the x-axis in the clockwise direction is negative of the tangent of the angle measured from the x-axis in the anticlockwise direction.