Question

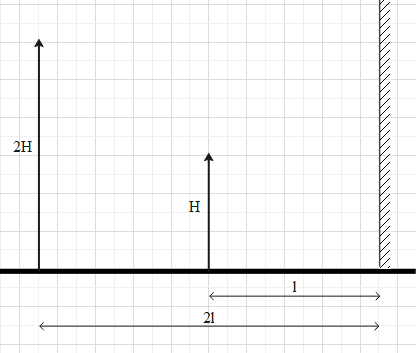
A child is standing in front of a straight plane mirror. His father is standing behind him, as shown in the fig. The height of the father is double the height of the child. What is the minimum length of the mirror required so that the child can completely see his own image and his father's image in the mirror? Given that the height of the father is 2H.

A. H/2
B. 5H/6
C. 3H/2
D. None of these

Answer 1

Hint: Know that the minimum length of the mirror, for the boy to his full image is half of his height. If the boy wants to see his father’s full image, then the light ray from the tip of his father must reflect at the top most point of the mirror and enter the boy’s eye. Therefore, draw a suitable ray diagram and find the length of the mirror with help of geometry.

Complete answer:
Here, if the boy wants to see his full image, i.e. form the bottom most point to the tip of his head then the minimum size of the mirror must be half of the boy height.
It is given that the height of the boy is H. Therefore, for the above case the length of the plane mirror must be at least equal to $\dfrac{H}{2}$.

However, it is given that the boy has to see his father’s full image too, who is standing behind the boy.
As you can see in the diagram, with the a mirror of length $\dfrac{H}{2}$, the boy can see the foot of his father, but he cannot see some of the upper part of his father. This means that the length of the mirror must be more than $\dfrac{H}{2}$. Let that extra length be x.

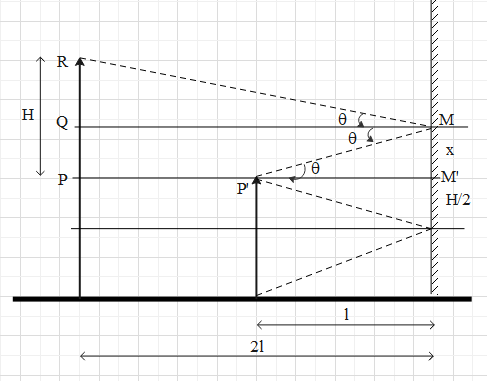
To see the tip of the head of his father, the light ray from the tip must reflect and enter the boy’s eye as shown.
According to the laws of reflection, $\angle RMQ=\angle PMQ=\theta $.
The length RP = H and QR = x.
Therefore, RQ = H-x.
In $\Delta RMQ$, $\tan \theta =\dfrac{RQ}{2l}=\dfrac{H-x}{2l}$ …. (i).
In $\Delta MP'M$, $\tan \theta =\dfrac{x}{l}$ ….. (ii).
From (i) and (ii) we get,
$\dfrac{H-x}{2l}=\dfrac{x}{l}$
$\Rightarrow H-x=2x$
$\Rightarrow x=\dfrac{H}{3}$.
Therefore, the total length of the mirror is $x+\dfrac{H}{2}=\dfrac{H}{3}+\dfrac{H}{2}=\dfrac{5H}{6}$.
This concludes that if the boy wants to see his full image as well as his father’s full image, then the length of the mirror must be more than $\dfrac{5H}{6}$, in the given case.

So, the correct answer is “Option B”.

Note:
If a man in front of a plane mirror wants to see his full image then the length of the mirror must be at least half of his height. The length of the mirror is independent of the distance between the man and the mirror.
However, in the given question, the length of the mirror depends on the distance between the people and the mirror.