Question

A chain of mass $m$ forming a circle of radius $R$ is slipped on a smooth round cone with half-angle $\theta $. Prove that the tension of the chain if it rotates with a constant angular velocity $\omega $ about a vertical axis coinciding with the symmetry axis of the cone is $T = \left( {\cot \theta + \dfrac{{{\omega ^2}R}}{g}} \right)\dfrac{{mg}}{{2\pi }}$.

Answer 1

Hint:Here we have to use Newton’s second law in projection form i.e, ${F_x} = m{\omega _x}$. If more than one torque operates along a fixed axis on a rigid body, the sum of the torques equals the moment of inertia times the angular acceleration.Torque is the measure of the force that can cause an object to rotate about an axis. Force is what causes an object to accelerate in linear kinematics.

Complete step by step answer:
Given, a chain of mass $m$ forming a circle of radius $R$ is slipped on a smooth round cone with half-angle $\theta $.

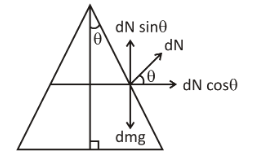
Each part of the chain acts on the necessary tensile stress. Therefore, we split the chain into thin, related elements in order to conclude that each element is a particle. We consider one such part of the mass $dm$ which at the middle subtends the angle $d\alpha $. With a recognised angular velocity, the chain travels around a circle of established radius $R$, and some forces act on it. We have to find one of these forces. Let us consider an element of mass $dN$.

Let its weight be $dmg$. The normal force on the cone is perpendicular. Let the angel be $\theta $. The components of the normal are $dN\sin \theta $ and $dN\cos \theta $. Let the angle formed by the radius of the circle on the circumference be $\alpha $ and the element formed is $d\alpha $.

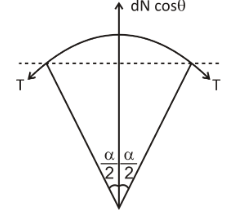
The element formed on the circle will be in the shape of a cone.
So, mass
$
dm = \dfrac{m}{{2\pi R}}Rd\alpha \\
\Rightarrow dm = \dfrac{m}{{2\pi }}d\alpha \\ $
Here, since the element is very small, we have taken $d\alpha $.
$
dN\sin \theta - gdm \\
\Rightarrow 2T\sin \dfrac{{d\alpha }}{2} = \left( {dN} \right)\cos \theta + dm{\omega ^2}R \\
\Rightarrow Td\alpha = gdm\dfrac{{cos\theta }}{{\sin \theta }} + dm{\omega ^2}R \\
\Rightarrow T\left( {\dfrac{{2\pi }}{m}} \right)dm = g\cot \theta dm + {\omega ^2}Rdm \\
$
$\therefore T = \left( {\cot \theta + \dfrac{{{\omega ^2}R}}{g}} \right)\dfrac{{mg}}{{2\pi }}$

Hence, it is proved.

Note:There may arise some confusion while writing the angles. So we have to be very careful while putting them in the formulae. Tension can be defined as an action-reaction pair of forces acting at each end of the said elements. While considering a rope, the tension force is felt by every section of the rope in both the directions, apart from the endpoints. The endpoints experience tension on one side and the force from the weight attached. Throughout the string, the tension varies in some circumstances.