Question

A Carnot refrigeration cycle absorbs heat at $270K$ and rejects heat at $300K$. If the cycle is absorbing $1260kJ/min$ at $270K$, then the work required per second is:
A. $2.33kJ/sec$
B. $4.66kJ/sec$
C. $1kJ/sec$
D. $4kJ/sec$

Answer 1

Hint: In the Carnot Cycle, heat flows from higher temperature to lower temperature without external work, naturally. But, by doing some work this can be reversed i.e., heat can be made to flow from low temperature to high temperature. The cycle obtained after reversing is called the Carnot refrigeration cycle.
Formula used:
$\dfrac{{dW}}{{dt}} = \dfrac{{d{Q_2}}}{{dt}} \times \dfrac{{{T_1} - {T_2}}}{{{T_2}}}$

Complete answer:
This Carnot Refrigerator Cycle represents a reverse heat engine cycle or a refrigerator cycle. It is drawn in the below diagram.

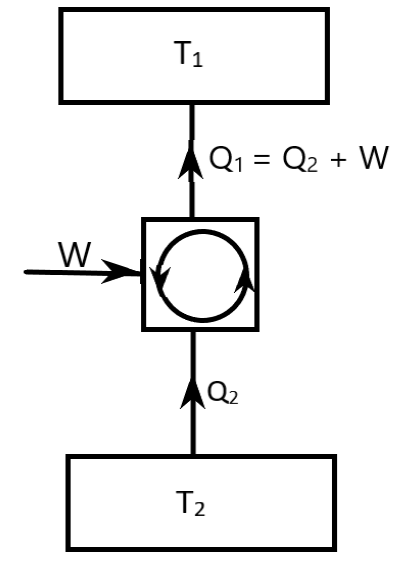
Here, ${T_2} < {T_1}$.
In the diagram,
${T_2}$ is the temperature of heat absorption
${T_1}$ is the temperature of heat rejection
${Q_2}$ is the heat absorbed
${Q_1}$ is the heat rejected
$W$ is the work done
The Coefficient of Performance of the refrigerator expresses the efficiency of the refrigerator. It is given by
$\eqalign{
  & {\left( {CO{P_{ref}}} \right)_{rev}} = \dfrac{{{Q_2}}}{W} = \dfrac{{{T_2}}}{{{T_1} - {T_2}}} \cr
  & \cr} $
From these numbers mentioned in that question, we have ${T_2} = 270K$ ,${T_1} = 300K$, $\dfrac{{d{Q_2}}}{{dt}} = 1260kJ/\min = 21kJ/\sec $
  Using this data and the above formula, we can find the work done required per second
$\eqalign{
  & \dfrac{{dW}}{{dt}} = \dfrac{{d{Q_2}}}{{dt}} \times \dfrac{{{T_1} - {T_2}}}{{{T_2}}} \cr
  & \Rightarrow \dfrac{{dW}}{{dt}} = 21kJ/\sec \times \left( {\dfrac{{300 - 270}}{{270}}} \right) = 2.33kJ/\sec \cr
  & \therefore \dfrac{{dW}}{{dt}} = 2.33kJ/\sec \cr} $

So, the correct answer is “Option A”.

Additional Information:
The Carnot refrigeration cycle is a graph drawn for Temperature vs Entropy.
Let us draw the graph to understand it better.

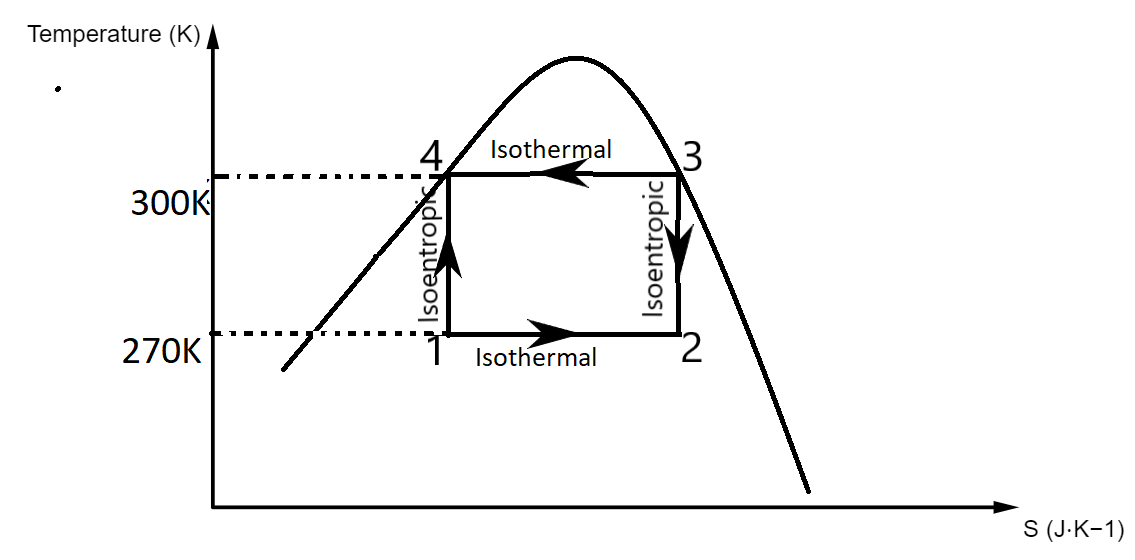
The curved part is called the Rankine curve.
In the graph,
1 to 2 denotes isothermal process
2 to 3 denotes isentropic process
3 to 4 denotes isothermal process

Note:
Don’t confuse Carnot Cycle for Carnot Refrigeration Cycle, both are contrary to each other. We can say that the Carnot refrigeration cycle is a reverse Carnot Cycle. The Carnot refrigeration cycle is a discipline of Thermal Prime Movers, an integral part of Mechanics. The COP is similar to that of the efficiency of a heat engine.