Question

A Carnot freezer takes heat from water at ${0^0}C$ inside it and rejects it to the room at a temperature of ${27^0}C$ The latent heat of ice is $336 \times {10^3}Jk{g^{ - 1}}$. If 5 kg of water at ${0^0}C$ is converted into ice at ${0^0}C$ by the freezer, then the energy consumed by the freezer is close to:
A. $1.51 \times {10^5}J$
B. $1.68 \times {10^6}J$
C. $1.71 \times {10^7}J$
D. $1.67 \times {10^5}J$

Answer 1

Hint: This is the question based on thermodynamics. There are two main devices used for heat transfer. They are heat engines and heat pumps. Refrigerators work on the same principle as the heat pump. We will calculate the coefficient of performance for the refrigerator and find out the energy consumed by the freezer.
Formula used:
$c.o.p = \dfrac{{{Q_L}}}{W} = \dfrac{{{Q_L}}}{{{Q_H} - {Q_L}}} = \dfrac{{{T_L}}}{{{T_H} - {T_L}}}$

Complete step-by-step solution:
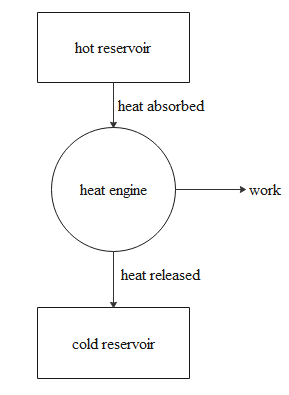
A heat engine is a device, which will take the heat from the hot body reservoir called a source and transfer the heat to the cool body reservoir which acts as a sink and does some work. No device will be hundred percent efficient so heat engines cannot convert the entire heat into work form. So some of the heat is lost to the sink and the rest is converted into work.
The entire mechanism of the heat engine is shown in the diagram below.

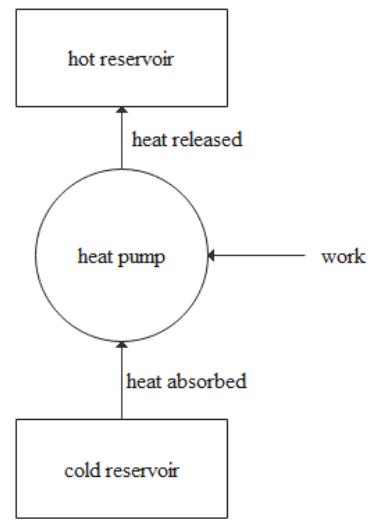
A heat pump is a device, which will take the heat from the cold body reservoir called that acts as a source and transfer the heat to the hot body reservoir which acts as a sink and consumes some work.
The entire mechanism of the heat pump is shown in the diagram below.

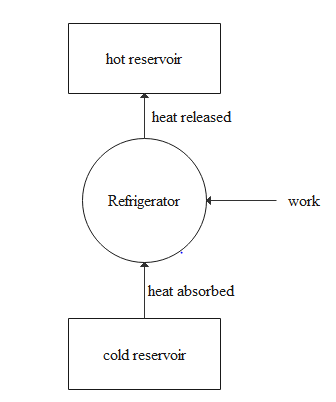
Refrigerators work on the principle of a heat pump. But the only difference is in the coefficient of performance of the heat pump and the refrigerator.

$c.o.p = {\text{desired output/work input}}$
 In the case of a heat pump, the desired output will be the heat given to the hot reservoir while in the case of a freezer the desired output will be the heat taken from the cold reservoir. Let the heat lost to the hot reservoir be ${Q_H}$ and the heat is taken from the cold reservoir be ${Q_L}$ then the work done will be $W = {Q_H} - {Q_L}$ and ${Q_H}$ will be proportional to ${T_H}$. ${Q_L}$ will be proportional to ${T_L}$. So the coefficient of performance of the refrigerator can be given as
$c.o.p = \dfrac{{{Q_L}}}{W} = \dfrac{{{Q_L}}}{{{Q_H} - {Q_L}}} = \dfrac{{{T_L}}}{{{T_H} - {T_L}}}$
$\eqalign{
  & \Rightarrow c.o.p = \dfrac{{273K}}{{300K - 273K}} \cr
  & \Rightarrow c.o.p = \dfrac{{273K}}{{27K}} \cr
  & \Rightarrow c.o.p = 10.12 \cr} $
Now the heat removed from the ice is
$\eqalign{
  & {Q_L} = mL \cr
  & \Rightarrow {Q_L} = 5 \times 336 \times {10^3} \cr} $
So the work to be done is
$W = \dfrac{{{Q_L}}}{{c.o.p}}$
$\eqalign{
  & \Rightarrow W = \dfrac{{5 \times 336 \times {{10}^3}}}{{10.12}} \cr
  & \Rightarrow W = 1.67 \times {10^5}J \cr} $
Hence option D will be the answer.

Note: Naturally heat transfers from the hot body to a cold body, but in the case of a refrigerator we are going against nature by transferring the heat from the low-temperature body to the high-temperature body, so we need to do some work on the refrigerator to get the required task done. That work is nothing but the electrical energy consumed by the refrigerator.