Question

A cardboard crate is 6 dm long, 3.4 dm wide and 3 dm high. Find its total surface area in $\text{c}{{\text{m}}^{2}}$ and $\text{d}{{\text{m}}^{2}}$. If the total crate surface is $\dfrac{5}{6}$ of the total cardboard surface used to construct the box, how much cardboard was used? \[\]

Answer 1

Hint: We recall the shape of a cuboid and its total surface area $A=2\left( lb+bh+hl \right)$ where $l$ is the length, $b$ is the breadth and $h$ is the height. Since the cardboard crate is of cuboids shape we use the formula for total surface area of cuboid to find and then convert it using $1\text{ dm}=10\text{ cm}$. We assume the total card board used as $x\text{ d}{{\text{m}}^{2}}$ whose ${{\left( \dfrac{5}{6} \right)}^{\text{th}}}$ is used to make the cardboard. We solve for $x$. \[\]

Complete step by step answer:
We know that a cuboid is a three dimensional object with six rectangular faces joined by 8 vertices. It has three different types of sides called length, breadth (also called width) and height denoted $l,$$b$ and $h$. The total surface area of a cuboid is the sum of areas of the rectangular faces which is given by;
\[A=2\left( lb+bh+hl \right)\]
We are given in the question a cardboard crate is 6 dm long, 3.4 dm wide and 3 dm high. So we
\[l=6\text{ dm},b=3.4\text{ dm},h=3\text{ dm}\]

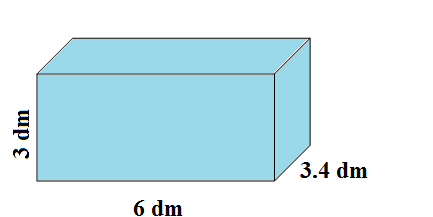
A cardboard crate is always made in cuboid shape. So the total surface area of the cardboard crate is
\[\begin{align}
  & A=2\left( lb+bh+hl \right) \\
 & \Rightarrow A=2\left( 6\times 3.4+3.4\times 3+3\times 6 \right) \\
 & \Rightarrow A=2\left( 20.4+10.2+18 \right) \\
 & \Rightarrow A=2\times 48.6=97.2\text{ d}{{\text{m}}^{2}} \\
\end{align}\]
We know that $1\text{ dm}=10\text{ cm}$. So we have $1\text{ d}{{\text{m}}^{2}}=1\text{ dm}\times \text{1dm =10 cm }\times \text{ 10 cm =100 c}{{\text{m}}^{2}}$. We use it to convert the total surface area of the cardboard crate as;
\[A=97.2\text{ d}{{\text{m}}^{2}}=97.2\times 100\text{ c}{{\text{m}}^{2}}=9720\text{ c}{{\text{m}}^{2}}\]
We are further given the question that the total crate surface is $\dfrac{5}{6}$ of the total cardboard surface used to construct the box and we are asked to find the total cardboard used. Let us assume that the total cardboard used is $x\text{ d}{{\text{m}}^{2}}$. Its’ ${{\left( \dfrac{5}{6} \right)}^{\text{th}}}$ will be used to make cardboard crate which will represent total surface area of the cardboard crate. So we have;
\[\begin{align}
  & x\times \dfrac{5}{6}=9720 \\
 & \Rightarrow x=\dfrac{6}{5}\times 9720=11664 \\
\end{align}\]

The amount cardboard used to make the cardboard crate is $11664\text{ d}{{\text{m}}^{2}}$.\[\]

Note: We note that the total cardboard crate surface is $\dfrac{5}{6}$ of total cardboard surface not the other way around. We can find the amount of wasted cardboard as $1-\dfrac{5}{6}=\dfrac{1}{6}$ of the total cardboard used $11664\text{ d}{{\text{m}}^{2}}$. We can find the volume of the empty space inside the cardboard crate as $V=lbh$ approximating the thickness of the cardboard as zero.