Question

A car is moving in a circular horizontal track of radius 10 m with a constant speed of $10\;{\rm{m}}{{\rm{s}}^{{\rm{ - 1}}}}$. A plumb bob is suspended from the roof of the car by a light rigid rod. The angle made by the rod with the vertical is
(A) Zero
(B) $30^\circ $
(C) $45^\circ $
(D) $60^\circ $

Answer 1

Hint: This question uses the concept of centripetal force and the force that pulls the object downwards. Firstly, you need to obtain two expressions for the forces acting in the horizontal direction and vertical direction. Then you need to divide the expressions, in order to calculate the angle from vertical.

Complete step by step answer:
We have the following data given in the question.
The radius of the circular track is 10 m.
The car is moving with the constant speed of $10\;{\rm{m}}{{\rm{s}}^{{\rm{ - 1}}}}$.

The acceleration due to the gravity is $g = 10\;{\rm{m}}{{\rm{s}}^{{\rm{ - 2}}}}$.
Let us assume that the angle made by the plumb bob from the vertical is $\theta $.

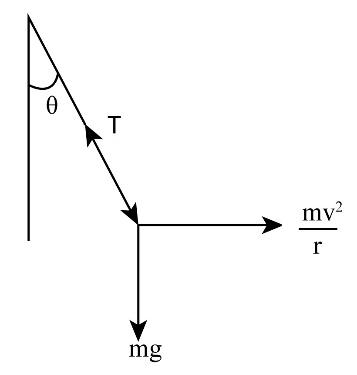
As the car is moving in a circular path, the centripetal force will be acting over the car in the outward direction. So, the expression that we will get along the horizontal direction is,
$T\sin \theta = \dfrac{{m{v^2}}}{r}.....\left( 1 \right)$

Similarly, the weight of the plumb bob will be acting in the downward direction. So, the expression for the forces along the vertical direction will be given as,
$T\cos \theta = mg......\left( 2 \right)$

From the above two expressions, we can easily evaluate the angle of the plumb bob from vertical.
Here we equate both equation (1) and (2),
$
\dfrac{{T\sin \theta }}{{T\cos \theta }} = \dfrac{{\dfrac{{m{v^2}}}{r}}}{{mg}}\\
\implies \tan \theta = \dfrac{{{v^2}}}{{rg}}
$

Substituting the numerical values in the above expression,
$
\tan \theta = \dfrac{{{v^2}}}{{rg}}\\
\implies \tan \theta = \dfrac{{{{\left( {10\;{\rm{m}}{{\rm{s}}^{{\rm{ - 1}}}}} \right)}^2}}}{{10\;{\rm{m}} \implies \times 10\;{\rm{m}}{{\rm{s}}^{{\rm{ - 2}}}}}}\\
\implies \tan \theta = 1
$

Further solving the equation,
$
\theta = {\tan ^{ - 1}}1\\
\implies \theta = 45^\circ
$

Therefore, the angle made by the plumb bob from vertical is $45^\circ $.

Therefore, the option (C) is the correct answer.

Note:
You need to solve this question by drawing the figure, or otherwise, you can make a mistake in obtaining the expressions.
Students can also calculate the answer by substituting the values in equation (1) and (2) individually and equate the values.