Question

A car accelerates from rest at a constant rate $\alpha$ for some time after which it decelerates at a constant rate $\beta$ to come to rest. If the total time elapsed is t, the maximum velocity acquired by the car is given by
$(a)\text{ }\left( \dfrac{{{\alpha }^{2}}+{{\beta }^{2}}}{\alpha \beta } \right)t$
$\begin{align}
  & (b)\text{ }\left( \dfrac{{{\alpha }^{2}}-{{\beta }^{2}}}{\alpha \beta } \right)t \\
 & (c)\text{ }\left( \dfrac{\alpha +\beta }{\alpha \beta } \right)t \\
 & (d)\text{ }\left( \dfrac{\alpha \beta }{\alpha +\beta } \right)t \\
\end{align}$

Answer 1

Hint: Assuming the maximum velocity, the one relation that relates all the given quantity is $v = u + at$. Using this and dividing the entire time span in two parts, the question can be solved easily.

Complete step by step answer:
Let us consider the car accelerates from rest at a constant rate $\alpha$ for time $t_{\alpha}$ to reach a maximum velocity of $v_{max}$. Therefore, we may write using the equation,

$v = u + at$

where, v is the final velocity, u is the initial velocity, a is the constant acceleration and t is the time taken. In this case,

$v = v_{max}, u = 0, a = \alpha, t = t_{\alpha}$

Therefore, we get,

$v_{max} = 0 + \alpha \times t_{\alpha}$ …(I)

Again, let us consider, the car decelerates from $v_{max}$ to rest at a constant rate of $\beta$ for time $t_{\beta}$. Hence, we have,

$v = 0, u = v_{max}, a = -\beta, t = t_{\beta}$

Therefore, we get,

$0 = v_{max} - \beta \times t_{\beta}$ …(II)

Drawing the car’s journey on a graph, we get

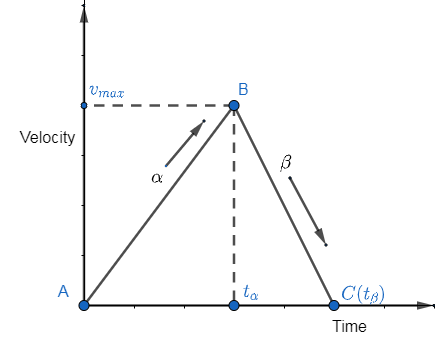
From the above graph, AB is the car's acceleration journey and BC is the decelerated journey.

From the question we know, the entire time taken is t, where $t = t_{\alpha}+t_{\beta}$. Solving Eq. (I) and (II) for $t_{\alpha}$ and $t_{\beta}$, we get,

$t_{\alpha} = \dfrac{v_{max}}{\alpha}$, $t_{\beta} = \dfrac{v_{max}}{\beta}$

Therefore, substituting this value in the below equation, we get

$t = t_{\alpha}+t_{\beta}$
$t = \dfrac{v_{max}}{\alpha} + \dfrac{v_{max}}{\beta}$

Now taking out the common term, we get

$t = v_{max}\left(\dfrac{1}{\alpha} + \dfrac{1}{\beta}\right)$

Taking LCM and solving, we get

$t = v_{max}\left(\dfrac{\alpha+\beta}{\alpha\beta}\right)$
$v_{max} = \left(\dfrac{\alpha\beta}{\alpha+\beta}\right)t$

Therefore, the correct option is D.

Note: If you look closely into the options, you would notice that they are of different dimensions. Hence, without even doing the sum, by performing a simple dimensional analysis, one can say the correct answer is D. It’s a trick that comes handy in a lot of such sums.