Question

A bullet of mass ${{m}_{2}}$ is fired from a gun of mass ${{m}_{1}}$ with horizontal velocity v. A plane mirror is fixed at gun facing the towards the bullet. The velocity of the image of the bullet formed by the plane mirror with respect to the bullet is?
$\text{A}\text{. }\left( 1+\dfrac{{{m}_{2}}}{{{m}_{1}}} \right)$
$\text{B}\text{. }\left( \dfrac{{{m}_{1}}+{{m}_{2}}}{{{m}_{1}}} \right)v$
$\text{C}\text{. 2}\left( \dfrac{{{m}_{1}}+{{m}_{2}}}{{{m}_{1}}} \right)v$
D. None of these

Answer 1

Hint: Apply the law of conservation of momentum and find the speed of the gun after the firing. Check what happens to the image when the mirror moves away from the object and the object also moves away from the mirror. Then find the speed of the image. Later, find the speed of the image with respect to the bullet.
Formula used:
P = mv
${{P}_{i}}={{P}_{f}}$

Complete answer:
It is given that a bullet is fired from a gun. Let us find the velocity of the gun.
For this we will apply the law of conservation of momentum because the net force on the system of the gun and the bullet is zero. The gun applies a force on the bullet and at the same time, the bullet also applies a force of equal magnitude but in the opposite direction.
According to the law of conservation of momentum, the initial momentum and the final momentum of the system is constant.
i.e. ${{P}_{i}}={{P}_{f}}$.
Momentum of a body of mass m moving with a velocity v is given as P=mv.
Since the gun and the bullet are at rest initially, the initial momentum of the system is zero.
$\Rightarrow {{P}_{i}}=0$.
After the firing, the velocity of the bullet is v. Let the speed of the gun u.
Therefore,
$\Rightarrow {{P}_{f}}={{m}_{1}}u+{{m}_{2}}v$
This means that
$\Rightarrow {{m}_{1}}u+{{m}_{2}}v=0$
$\Rightarrow u=-\dfrac{{{m}_{2}}}{{{m}_{1}}}v$.
This means that the gun moves in the opposite direction of the bullet with a speed of $\dfrac{{{m}_{2}}}{{{m}_{1}}}v$.
Since the mirror is attached to the gun, the mirror will also move in the opposite direction of the bullet with a speed of $u=\dfrac{{{m}_{2}}}{{{m}_{1}}}v$.
When the mirror moves away from a stationary object with speed u, the image of the object moves with speed 2u in the direction of motion of the mirror.
When an object moves away from a stationary mirror with speed v, its image also moves away from the mirror with speed v.

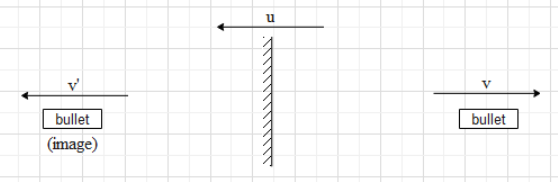
In this case, both scenarios are taking place. Therefore, the speed of the image will be $v'=v+2u$ and it is moving away from the mirror (in the direction along the direction of motion of the mirror).
$\Rightarrow v'=v+2\left( \dfrac{{{m}_{2}}}{{{m}_{1}}} \right)v$
$\Rightarrow v'=\left( 1+\dfrac{2{{m}_{2}}}{{{m}_{1}}} \right)v$.
v’ is the speed of the image with respect to a stationary observer.
Since the bullet is moving in the opposite direction to the direction of motion of the image, the speed of the image with respect to the bullet is $v'+v=\left( 1+\dfrac{2{{m}_{2}}}{{{m}_{1}}} \right)v+v=2\left( \dfrac{{{m}_{1}}+{{m}_{2}}}{{{m}_{1}}} \right)v$.

Hence, the correct option is C.

Note:
Note that when the mirror moves towards a stationary object with speed u, the image of the object moves with speed 2u in the direction of motion of the mirror.
When an object moves towards a stationary mirror with speed v, its image also moves towards the mirror with speed v. Meaning, both the object and the image move towards each other.