Question

A bucket open at the top, and made up of a metal sheet is in the form of a frustum of a cone. The depth of the bucket is 24 cm and the diameters of its upper and lower circular ends are 30 cm and 10 cm respectively. Find the cost of the metal sheet used in it at the rate of Rs. 10 per 100 $cm^2$. (Use $\pi = 3.14$). Insert answer is the nearest integer.
               

Answer 1

Hint: We will first mark the measure in the figure. Now, to construct a bucket, we obviously require the surface area of all the part that is the bottom circle, the upper circle and the frustum in between, we will calculate all that using the formulas required and add them and calculate the cost accordingly.

Complete step-by-step answer:
We have with us :
               

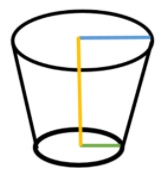
Now, since we are given the depth of the bucket is 24 cm and the diameters of its upper and lower circular ends are 30 cm and 10 cm respectively. Since, the lines in blue and green are the radii, so it will be half of the diameters. $\left( {Radius = \dfrac{{Diameter}}{2}} \right)$
So, the yellow line will be 24 cm long, which is the height of frustum. The blue and green lines will be 15 cm and 5 cm respectively.
Now, let us find the area of the lower circle only because the bucket is open at the top. So, no sheet is used there.
We know that the area of a circle is given by $A = \pi {r^2}$, where r is the radius of the circle.
Hence, the area of the bottom circle is $A = \pi {r^2} = 3.14 \times 5 \times 5 = 78.5$ $cm^2$ (Because $\pi = 3.14$) …….(1)
Now, we know that area of a frustum is given by $A = \pi ({r_1} + {r_2})l$, where ${r_1} + {r_2}$ is sum of both the radii upper and lower and l is the slant height of the frustum.
Now to apply this formula, we need to find l that is the slant height.
Using the formula for l that is $l = \sqrt {{{({r_1} - {r_2})}^2} + {h^2}} $ where h is the depth of the frustum.
So, $l = \sqrt {{{(15 - 5)}^2} + {{24}^2}} = \sqrt {100 + 576} = \sqrt {676} = 26cm$.
So, now putting these values in $A = \pi ({r_1} + {r_2})l$, we will get:-
$A = \pi ({r_1} + {r_2})l = 3.14 \times (15 + 5) \times 26 = 1632.9$ $cm^2$.
So, the total surface area of the bucket is (1632.9 + 78.5) $cm^2 $. That is 1711.4 $cm^2$.
Now, we have been given that for 100 $cm^2$ the cost is Rs. 10.
So, for 1 $cm^2$ the cost will be $Rs.\dfrac{{10}}{{100}} = Rs.\dfrac{1}{{10}}$.
So, for $1632.9$ $cm^2$, the cost will be $Rs.\dfrac{1}{{10}} \times 1711.4 = Rs.171.14$.
Hence, the cost will be Rs. 171.14.
The nearest integer to it will be Rs. 171.


Note: The students might make the mistake of using $\pi = \dfrac{{22}}{7}$ instead of $\pi = 3.14$ which will change the values a bit. So, take care regarding that. See if some particular value is mentioned, use that only. Otherwise, it is up to you.
The students might make the mistake of using height in the formula of area of frustum because slant height is also an height but remember slant height is the line joining the boundary of both the circle and height/ depth is the line joining the centers of the circles.