Question

A bucket of height 16cm is made up of metal sheet in the form of frustum of right circular cone with radii of its lower end upper ends as 8cm and 20cm respectively. Find the volume of milk which can be filled in the bucket. Also find the cost of making the bucket when the metal sheet costs Rs.15 per $100cm^2$.

Answer 1

Hint: In this question we need to find the volume and the outer surface area of the bucket. In order to do this, we will firstly find the slant height of the bucket and then use the formulas of surface area and volume for frustum. This will help us reach the answer.

Complete step-by-step answer:

We have been given that the height of the bucket is 16cm, with radii of its lower end upper ends as 8cm and 20cm respectively.
So, let h = 16cm, R = 20cm, r = 8cm

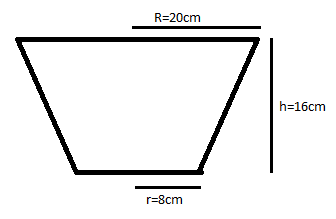
As a bucket has a shape of a frustum. So, let l be the slant height of frustum

Now, as we know in a frustum, $l = \sqrt {{h^2} + {{\left( {R - r} \right)}^2}} $

So, $l = \sqrt {{{16}^2} + {{\left( {20 - 8} \right)}^2}} $
$ \Rightarrow l = \sqrt {256 + 144} = 20cm$.

Now, the surface area of the bucket = Surface area of frustum + Surface Area of the base

And the surface area of frustum = $\pi l\left( {R + r} \right)$
=$\pi \times 20\left( {20 + 8} \right) = 1760c{m^2}$

Hence, the total metal sheet required.
= $1760 + \dfrac{{22}}{7} \times {8^2}$
$ = 1961.14c{m^2}$

Now, the total cost of the metal sheet will be = $191.14 \times \dfrac{{15}}{{100}} = Rs.294.17$
Now, we need to find the volume of the bucket = Volume of cone with radius R - Volume of cone with radius R
=\[\dfrac{{\pi h\left( {{R^3} - {r^3}} \right)}}{3}\]
$ = \dfrac{{\pi \times 16\left( {{{20}^3} - {8^3}} \right)}}{3}$
$ = \dfrac{{22 \times 16 \times 7488}}{{7 \times 3}}$
$ = 1,25,513.14c{m^3}$

So, 125.513L of milk can be stored in the bucket.

Note: Whenever we face such types of problems the key point to remember is that we need to have a good grasp over surface area and volumes. In these types of questions, we should always firstly find the slant height of the cone/frustum which can help you in simplification and getting on the right track to reach the answer.