Question

When a bucket containing water is rotated fast in a vertical circle of radius $R$ , the water in the bucket doesn’t spill provided:
A. The bucket is whirled with a maximum speed of $\sqrt{2gR}$
B. The bucket is whirled around with a minimum speed of $\sqrt{\dfrac{gR}{2}}$
C. The bucket is having a rpm of $\sqrt{\dfrac{900g}{\pi^{2}R}}$
D. The bucket is having a rpm of $\sqrt{\dfrac{3600g}{\pi^{2}R}}$

Answer 1

Hint: Here, it is given that we are trying to rotate a bucket containing some water in a vertical circle, then to avoid the water from falling from the bucket, the force due to gravity which is acting on the water must be equal to the centripetal force acting on the bucket. Using this equation, we can solve the question to identify the necessary and required condition.
Formula used:
$F_{c}=\dfrac{mv^{2}}{r}$

Complete answer:
To begin with let us assume that the mass of the bucket with the water is say $M$. Then the force due to gravity acting on the bucket with the water is given as $F_{g}=Mg$, where $g$ is the acceleration due to gravity.
Since the bucket is also moving in a vertical circle, with some constant velocity, say $v$ then the centripetal force due the circular motion is given as $F_{c}=\dfrac{Mv^{2}}{R}$, where $R$ is the radius of the vertical circle, as given in the question. Consider the figure shown below, to understand the direction of the forces.

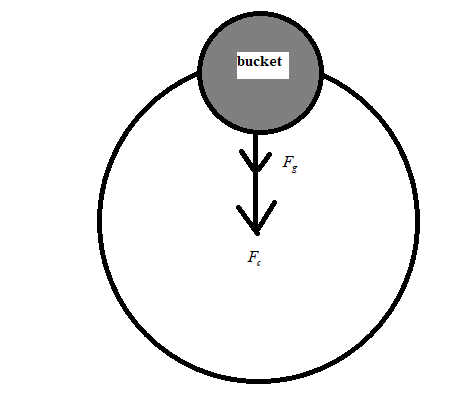
Clearly, to avoid the water from falling from the bucket, the two forces acting on the bucket must be equal. Thus, we have $F_{g}=F_{c}$
$\implies Mg=\dfrac{Mv^{2}}{R}$,
$\implies g=\dfrac{v^{2}}{R}$
$\implies v=\sqrt{gR}$
Let us assume that the angular velocity due to the circular motion is given as $\omega$. Then from the definition of angular velocity ,$\omega=\dfrac{v}{R}$ also we know that $\omega=2\pi\nu$. Then, we have $\omega=\dfrac{\sqrt{gR}}{R}$
$\implies \omega=\sqrt{\dfrac{g}{R}}$
$\implies 2\pi\nu=\sqrt{\dfrac{g}{R}}$
$\implies v=\sqrt{\dfrac{g}{4\pi^{2}R}}$
In terms of rpm, we have $v=\sqrt{\dfrac{g}{4\pi^{2}R}}\times 60$
$\implies v=\sqrt{\dfrac{3600g}{4\pi^{2}R}}$
$\therefore v=\sqrt{\dfrac{900g}{\pi^{2}R}}$
Thus the minimum velocity required to avoid the water from falling is given as $v=\sqrt{\dfrac{900g}{\pi^{2}R}}$

Hence the correct answer is option C. the bucket is having a rpm of $\sqrt{\dfrac{900g}{\pi^{2}R}}$

Note:
Here, we equate the two forces acting on the bucket, to ensure that the water in the bucket is in equilibrium. This is important, to avoid the water from falling from the bucket. Also revolution per minute (rpm) is nothing but the number of rotations or turns made by the bucket in the vertical circle in one minute.