Question

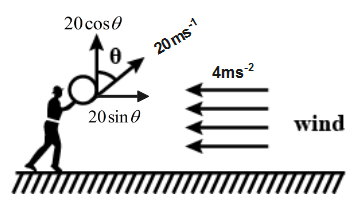
A boy throws a ball upwards with velocity \[{{V}_{0}}=20m{{s}^{-1}}\].The wind imparts a horizontal acceleration of \[4m{{s}^{-2}}\]to the left .The angle \[\theta \] at which the ball must be thrown so that the ball returns to the boy’s hand is\[(g=10m{{s}^{-2}})\].

\[A){{\tan }^{-1}}(1.2)\]
\[B){{\tan }^{-1}}(2.5)\]
\[C){{\cot }^{-1}}(2)\]
\[D){{\cot }^{-1}}(2.5)\]

Answer 1

Hint: When a ball is thrown with some velocity it has two components of velocity one is responsible for horizontal motion and one is responsible for vertical motion. Since air acceleration is acting in horizontal direction so only horizontal motion is affected due to this air acceleration and comes to the initial point from where it is started.

Complete answer:
Since ball is thrown with velocity
\[20m{{s}^{-1}}\] at an angle
\[\theta \]with vertical.
So velocity of ball can be resolved in two components: -
1. Vertical Component
\[{{V}_{y}}=20Cos\theta \].
2. Horizontal Component
\[{{V}_{x}}=20Sin\theta \].
For Vertical Motion,
Vertical component of velocity will take the ball upwards and it gets back to hand of man so air acceleration is not working while dealing with vertical direction.
Let us assume total time of flight taken by vertical direction to get the ball back in the hands of man is t.
So we apply first equation of motion,
\[v=u+at\]
as ball reaches the maximum height till it final velocity becomes zero so
\[v=0\]
Initial velocity of ball in vertical motion is,
\[u={{V}_{y}}\].
Acceleration of gravity always acts in a downward direction.
Time to reach the highest point and then returning back to the initial point is the same. So total time of flight is represented as
\[t=\dfrac{2{{V}_{y}}}{g}\]
\[t=\dfrac{40Cos\theta }{g}\]
\[t=\dfrac{40Cos\theta }{10}\]
\[t=4Cos\theta \]\[(Equation1)\]
For horizontal motion,
Ball is moving with horizontal component of velocity
\[20Sin\theta \]
but air acceleration is acting in the right direction so due to this air acceleration the ball gets back to the initial point so displacement of the ball along horizontal becomes 0.
So we apply Second equation of motion,
Since displacement is 0 and we already calculated the time to reach the starting point in equation 1.
Since direction of acceleration is in the opposite direction of horizontal velocity so it is taken as negative in direction.
\[{{a}_{x}}=-4m{{s}^{-2}}\]
So we get
\[S=ut+\dfrac{1}{2}a{{t}^{2}}\]
\[0={{V}_{x}}t+\dfrac{1}{2}{{a}_{x}}{{t}^{2}}\]
\[0=20Sin\theta t-\dfrac{1}{2}4{{t}^{2}}\]
\[20Sin\theta t=2{{t}^{2}}\]
\[t=10Sin\theta \]\[(Equation2)\]
from equation 1 and Equation 2, we get
\[4Cos\theta =10Sin\theta \]
\[\Rightarrow \]\[Tan\theta =\dfrac{4}{10}\]
\[\Rightarrow Cot\theta =\dfrac{10}{4}\]
\[\therefore \]\[\theta =Co{{t}^{-1}}(2.5)\]
So the ball must be thrown at angle \[Co{{t}^{-1}}(2.5)\] so that the ball will return to the boy's hand.

Correct Option is D.

Note:
The main point to notice in this question is that horizontal displacement becomes 0 because air acts in the opposite direction and the ball comes to the initial position again. The value of acceleration due to gravity is taken as negative when the body is going away from earth and it is taken as positive when the body is coming back to earth.