Question

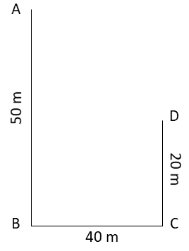
A boy moves along the path ABCD. What is the total distance covered by the boy? What is his net displacement?

Answer 1

Hint: Recall the basics of the total distance covered by an object and displacement of an object. The total displacement of the object is the total distance travelled by the object and displacement of the object is the shorted distance between the initial and final point of motion of the object. Using this information, calculate the total distance covered and displacement by the boy.

Complete step by step answer:
We have given that the boy is moving along the path ABCD. We have asked to determine the total distance covered by the boy and displacement of the boy. The total distance covered by the boy is the sum of all distances travelled by the boy. Here, the distances covered by the boy are AB, BC and CD. Hence, the total distance travelled by the boy is
\[{\text{Distance}} = {\text{AB}} + {\text{BC}} + {\text{CD}}\]

Substitute \[50\,{\text{m}}\] for \[{\text{AB}}\], \[40\,{\text{m}}\] for \[{\text{BC}}\] and \[20\,{\text{m}}\] for \[{\text{CD}}\] in the above equation.
\[{\text{Distance}} = \left( {50\,{\text{m}}} \right) + \left( {40\,{\text{m}}} \right) + \left( {20\,{\text{m}}} \right)\]
\[ \Rightarrow {\text{Distance}} = 110\,{\text{m}}\]
Hence, the total distance covered by the boy is \[110\,{\text{m}}\].

Let us now determine the displacement of the boy. Redraw the given diagram as follows:

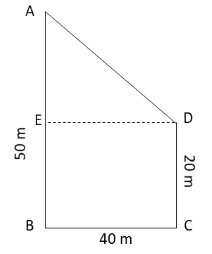
The shortest distance between the point A and D is AD. Hence, the displacement of the boy is given by AD. Let us first determine the values of AE and DE.
From the above diagram,
\[{\text{BE}} = {\text{CD}} = 20\,{\text{m}}\]
\[{\text{BC}} = {\text{DE}} = 40\,{\text{m}}\]
And
\[{\text{AE}} = {\text{AB}} - {\text{BE}}\]
\[ \Rightarrow {\text{AE}} = {\text{AB}} - {\text{CD}}\]
Substitute \[50\,{\text{m}}\] for \[{\text{AB}}\] and \[20\,{\text{m}}\] for \[{\text{CD}}\] in the above equation.
\[ \Rightarrow {\text{AE}} = \left( {50\,{\text{m}}} \right) - \left( {20\,{\text{m}}} \right)\]
\[ \Rightarrow {\text{AE}} = 30\,{\text{m}}\]

Let us now apply Pythagoras theorem to the triangle AED in the above figure.
\[{\text{A}}{{\text{D}}^{\text{2}}} = {\text{A}}{{\text{E}}^{\text{2}}} + {\text{D}}{{\text{E}}^2}\]
Substitute \[30\,{\text{m}}\] for \[{\text{AE}}\] and \[40\,{\text{m}}\] for \[{\text{DE}}\] in the above equation.
\[{\text{A}}{{\text{D}}^{\text{2}}} = {\left( {30\,{\text{m}}} \right)^{\text{2}}} + {\left( {40\,{\text{m}}} \right)^2}\]
\[ \Rightarrow {\text{A}}{{\text{D}}^{\text{2}}} = 900 + 1600\]
\[ \Rightarrow {\text{A}}{{\text{D}}^{\text{2}}} = 2500\]
\[ \therefore {\text{AD}} = 50\,{\text{m}}\]
Hence, the displacement of the boy is \[50\,{\text{m}}\].

Hence, the total distance travelled and displacement of the boy are \[110\,{\text{m}}\] and \[50\,{\text{m}}\] respectively.

Note:One can also solve the same question by another method. One can first obtain the position vectors of the boy at points A and D for determining the displacement of the boy. Then use the law of triangle and apply it to the triangle formed by the motion of the boy to determine the value of the AD vector to determine the value of displacement of the boy.