Question

A box of mass 1 kg starts to move up on a frictionless inclined plane of inclination 30° with an acceleration ${a_0 }$ = 3 m/s² by applying a constant force F along the inclined plane. When a block of mass ${m_0} $ is put inside the box, the box slides down with the same acceleration ${a_0} $. The value of ${m_0}$ is
(A) $1\;{\rm{kg}}$
(B) $2\;{\rm{kg}}$
(C) $3\;{\rm{kg}}$
(D) $4\;{\rm{kg}}$

Answer 1

Hint:
When an object moves on an inclined plane, then the object applies some force on the surface due to the weight of the object. The applied force has two components: the one works along the surface of the plane and the other works perpendicular to the plane.

Complete step-by-step solution:
The mass of the box is: $m = 1\;{\rm{kg}}$
The angle of the inclined plane is: $\theta = 30^\circ $
The acceleration of the object along the surface of the inclined plane is : ${a_0} = 3\;{m {\left/
 {\vphantom {m {{s^2}}}} \right.
 } {{s^2}}}$
The schematic diagram of the system is given as follows,

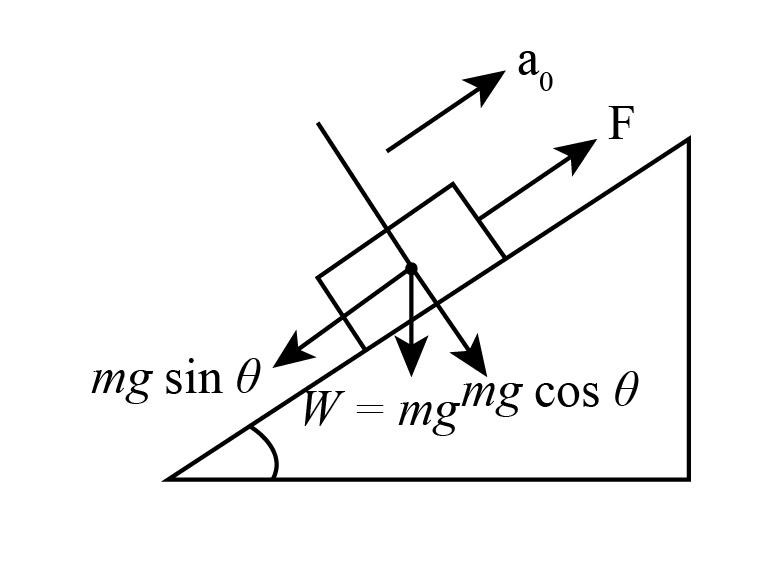
Here we can see that there is a component of the weight, that is working just opposite to the force $F$ .
- Now we balance the force along the surface of inclined plane,
$
\Rightarrow F - mg\sin \theta = m{a_0}\\
\Rightarrow F = mg\sin \theta + m{a_0}.............{\rm{(1)}}
$
- Now we put the mass ${m_0}$ in the box, and now the total mass of the box is :$m + {m_0}$
- Now the component of the force along the surface of the inclined plane due to the weight of the box becomes $\left( {m + {m_0}} \right)g\sin \theta $.
As the box slides down with the same acceleration ${a_0}$ after the addition of mass ${m_0}$, the component of the force along the surface of the inclined plane due to the weight of the box will be more than the force $F$.
- Now we will again balance the force along the surface of inclined plane,
$\left( {m + {m_0}} \right)g\sin \theta - F = \left( {m + {m_0}} \right){a_0}..........{\rm{(2)}}$
- Substitute the value of $F$ from equation(1) in the equation (2),
$
\Rightarrow \left( {m + {m_0}} \right)g\sin \theta - \left( {mg\sin \theta + m{a_0}} \right) = \left( {m + {m_0}} \right){a_0}\\
\Rightarrow {m_0}g\sin \theta - m{a_0} = m{a_0} + {m_0}{a_0}\\
\Rightarrow {m_0}g\sin \theta - {m_0}{a_0} = 2m{a_0}
$
Solve further,
$ \Rightarrow {m_0} = \dfrac{{2m{a_0}}}{{g\sin \theta - {a_0}}}$
Taking The acceleration due to the gravity is:$g = 10\;{m {\left/
 {\vphantom {m {{s^2}}}} \right.
 } {{s^2}}}$
- Substitute all the values in the above expression,
$ \Rightarrow {m_0} = \dfrac{{2 \times 1 \times 3}}{{10 \times \sin 30^\circ - 3}}$
It is known that \[\sin 30^\circ = \dfrac{1}{2}\] , so substitute the value of \[\sin 30^\circ \],
$
\Rightarrow {m_0} = \dfrac{{2 \times 1 \times 3}}{{10 \times \dfrac{1}{2} - 3}}\\
\Rightarrow {m_0} = \dfrac{6}{2}\\
\Rightarrow {m_0} = 3\;{\rm{kg}}$

Therefore, the value of ${m_0}$ is $3\;{\rm{kg}}$, and
the correct answer is option (C).

Note:
In such a type of question, If the friction is present between the surface of the inclined plane and the object, then we will consider the friction force and this force will act opposite to the direction of the motion of the object.