Question

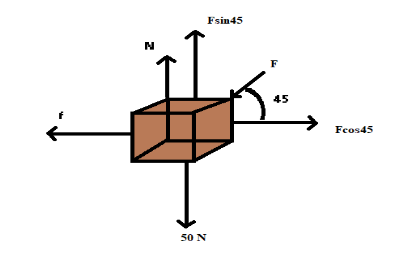
A body of weight \[50{\text{ N}}\]placed on a horizontal surface is just moved by a force of\[28.2{\text{ N}}\]. The frictional force and Normal reaction are:

(A) \[2{\text{ N, 3 N}}\]
(B) \[{\text{5N, 6N}}\]
(C) \[10{\text{N, 15N}}\]
(D) \[2{\text{0N, 30N}}\]

Answer 1

Hint:Free body diagram is used to recognize all the forces acting on the object, and force acting at an angle on the object should be resolved in vertical and horizontal direction to evaluate the desired result.

Formula used:
Write down the summation of forces acting in the horizontal direction for equilibrium.
$\sum {{F_h} = 0} $
Write down the summation of forces acting in the vertical direction for equilibrium.
$\sum {{F_v} = 0} $

Complete step by step answer:
Understand that force is applied at an angle \[{45^\circ }\]from the horizontal direction. The components of forces are resolved in the horizontal and vertical direction of the body.

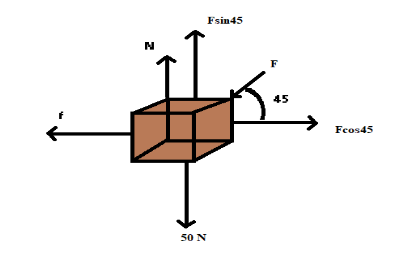
Here, \[N\] is the normal reaction force, \[F\sin {45^\circ }\] is the vertical component of the force applied, \[f\] is the frictional force acting due to motion of body and \[F\cos {45^\circ }\] is the horizontal component of the force.
Write down the summation of forces acting in the horizontal direction for equilibrium.
$
\sum {{F_h} = 0} \\
\Rightarrow F\cos {45^\circ } - f = 0 \\
$
Here, ${F_h}$ is force acting in the horizontal direction.
Rearrange for \[f\]
$f = F\cos {45^\circ }$
Substitute \[28.2\,{\text{N}}\] for \[F\] and \[\dfrac{1}{{\sqrt 2 }}\] for $\cos {45^\circ }$
$
f = (28.2{\text{ N)}}\dfrac{1}{{\sqrt 2 }} \\
\Rightarrow f= 19.94{\text{ N}} \\
\approx {\text{20 N}} \\
$
Write down the summation of forces acting in the vertical direction for equilibrium.
$
\sum {{F_v} = 0} \\
\Rightarrow F\sin {45^\circ } + N - 50\;{\text{N}} = 0 \\
$
Here, ${F_v}$ is force acting in the vertical direction.
Rearrange for $N$
$N = 50\;{\text{N}} - F\sin {45^\circ }$
Substitute \[28.2\,{\text{N}}\] for \[F\] and \[\dfrac{1}{{\sqrt 2 }}\] for $\sin {45^\circ }$
$
N = 50\;{\text{N}} - 28.2(\dfrac{1}{{\sqrt 2 }}) \\
\approx 30{\text{ N}} \\
$
Therefore, Option D is the correct choice.

Note:Free body diagram is drawn to find out the net forces acting in the horizontal and vertical direction. The net force acting in the horizontal and vertical direction are considered to be zero for equilibrium condition. The forces acting in the vertical direction give us the value of normal reaction and forces acting in the horizontal direction give us the value of frictional force.