Question

A body of mass $m$ is moved to a height equal to the radius of the earth $R$ (above the surface). The increase in its potential energy is
A) $mgR$
B) $2mgR$
C) $\dfrac{1}{2}mgR$
D) $\dfrac{1}{4}mgR$

Answer 1

Hint: The potential energy, in this case, is actually the work done against the gravitational force. The gravitation being a central force depends on the distance between the center of the mass of the two bodies; here, which are the body of mass $m$ and the earth. Here you can neglect the dimension of the object with respect to the earth and consider it as a point object. As the potential energy due to gravitation is attractive in nature, hence here the potential energy is negative which means you have to work upon the body to move it against the gravitation.

Formula used:
The gravitational potential $U$ of a body of mass $m$ due to a body of mass $M$ at a distance $R$ is
$U = - \dfrac{{GMm}}{R}$ …………….(1)
where $G$ is the universal gravitational constant.
You know that the acceleration due to gravity on the surface of the earth on anybody is denoted as $g$, so a body of mass $m$ on the surface of earth feels a force due to gravity as
$F = mg$ ……..(2)
Now you know the gravitational force between earth and a body of mass $m$ on the surface can be expressed as
$F = \dfrac{{G{M_e}m}}{{{R_e}^2}}$ …………...(3)
Hence, you can see from eq (2) and eq (3)
$
  mg = \dfrac{{Gm{M_e}}}{{{R_e}^2}} \\
   \Rightarrow g = \dfrac{{G{M_e}}}{{{R_e}^2}} \\
 $ …………..(4)

Complete step by step answer:
Given:
The mass of the object is $m$.
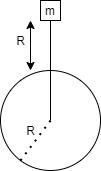
The radius of the earth is $R$.
The mass is moved to height $R$ from the surface of the earth.
To find: The increment in the potential difference of the body.

Step 1:
You can write the potential energy of the body with mass $m$ on the surface of the earth from eq (1) as
${U_i} = - \dfrac{{G{M_e}m}}{R}$ ………... (5)
Where ${M_e}$ is the mass of the earth.
Step 2:
The dimension of the object being negligible to the earth, you can take the object as a point object. Now you can see that when the body is moved up to height $R$ from the surface the distance of the body from the center of the earth is $\left( {R + R} \right) = 2R$.
So, the new potential energy of the body becomes from the eq (1)
${U_f} = - \dfrac{{G{M_e}m}}{{2R}}$ ………...(6)

Step 3:
You can calculate the increase in the potential of the body by subtracting eq (6) from eq (1)
$ \Delta U = {U_f} - {U_i} = - \dfrac{{G{M_e}m}}{{2R}} - \left( { - \dfrac{{G{M_e}m}}{R}} \right) $
$ = - \dfrac{{G{M_e}m}}{{2R}} + \dfrac{{G{M_e}m}}{R} $
$ = \dfrac{{G{M_e}m}}{{2R}} $

Step 4:
Now express the increment of the potential energy of the body in terms of the gravitational acceleration on the surface of the earth $g$ by using eq (4).
$\Delta U = \dfrac{{G{M_e}m}}{{2R}} = \dfrac{{G{M_e}m}}{{2{R^2}}}R = \dfrac{{mgR}}{2}$

If a body of mass $m$ is moved to a height equal to the radius of the earth $R$ (above the surface, then the increase in its potential energy is $\dfrac{1}{2}mgR$. Hence, (C) is the correct option.

Note:
There are two crucial points which you should be careful of. Firstly, gravitation is attractive in nature and hence, the potential should be negative. Gravitation is a central force. So, its dependence is on the distance between the centers. So, be careful to take the distance from the center not from the surface of the earth, that is $\left( {R + R} \right) = 2R$.
There can be another error if the approach of direct calculation of the potential energy is taken. Then taking the earth’s surface as ground label, the potential on the surface of earth cannot be calculated as $\Delta U = mgR$ as the value of the gravitational acceleration is continuously changed from $g$ to $g{\left( {\dfrac{R}{{R + R}}} \right)^2} = g{\left( {\dfrac{1}{2}} \right)^2} = \dfrac{g}{4}$, which you can see as for at a height $h$ from the surface of the earth the acceleration due to gravity changes as $g' = g{\left( {\dfrac{R}{{R + h}}} \right)^2}$.