Question

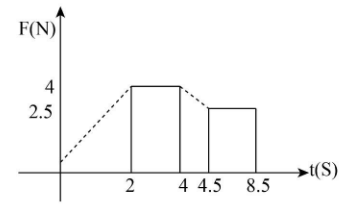
A body of mass \[2{\rm{ kg}}\] has an initial speed \[5{\rm{ m}}{{\rm{s}}^{ - 1}}\]. A force acts on it for 4 seconds in the direction of motion. The force time graph is shown in figure. The final speed of the body is

1) \[8.5{\rm{ m}}{{\rm{s}}^{ - 1}}\]
2) \[11{\rm{ m}}{{\rm{s}}^{ - 1}}\]
3) \[14.31{\rm{ m}}{{\rm{s}}^{ - 1}}\]
4) \[4.31{\rm{ m}}{{\rm{s}}^{ - 1}}\]

Answer 1

Hint:The area of force-time curve of the given body gives us the value of change in momentum of the body. We know that the momentum of the body is equal to the product of its mass and velocity. We will use these concepts to deduce the final velocity of the given body.

Complete step by step answer:
Given:
The mass of the body is \[m = 2{\rm{ kg}}\].
The initial speed of the body is \[{V_i} = 5{\rm{ m}}{{\rm{s}}^{ - 1}}\].
The time for action of the force is \[t = 4{\rm{ s}}\].
We know that the area of the force-time graph gives us the value of change in momentum of the body. By closely observing the graph we will find that there are two triangles and the rest are rectangles. We know that the area of a triangle is the half of the product of its base and height and the product of two adjacent sides gives the area of a rectangle. Therefore, we can write the area of the given graph to know the difference between the initial and final of the given body as below:
\[
\Delta P = \left( {\dfrac{1}{2} \times 2 \times 4} \right) + \left[ {\left( {4 - 2} \right) \times 4} \right] + \left[ {\left( {4.5 - 4} \right) \times 2.5} \right] + \left[ {\dfrac{1}{2}\left( {4.5 - 4} \right)\left( {4 - 2.5} \right)} \right] + \left[ {\left( {8.5 - 4.5} \right) \times 2.5} \right]\\
\Rightarrow\Delta P = 23.625
\]
We know that the momentum of a body is given by the product of its mass and velocity; therefore, its unit is kilogram-metre per second so that we can write:
\[\Delta P = 23.625{\rm{ kgm}}{{\rm{s}}^{ - 1}}\]
We can also write the above expression as the difference between final and initial momentum.
\[
{P_f} - {P_i} = 23.625{\rm{ kgm}}{{\rm{s}}^{ - 1}}\\
\Rightarrow{P_f} = 23.625{\rm{ kg}}{{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {\rm{s}}}} \right.
 } {\rm{s}}} + {P_i}
\]……(1)
Here \[{P_f}\] is the final momentum and \[{P_i}\] is the initial momentum.
Let us write the expression for the initial momentum of the body.
\[{P_i} = m{V_i}\]
On substituting \[2{\rm{ kg}}\] for m and \[5{\rm{ m}}{{\rm{s}}^{ - 1}}\] for \[{V_i}\] in the above expression, we get:
\[
{P_i} = \left( {2{\rm{ kg}}} \right)\left( {5{\rm{ m}}{{\rm{s}}^{ - 1}}} \right)\\
\Rightarrow{P_i} = 10{\rm{ kgm}}{{\rm{s}}^{ - 1}}
\]
On substituting \[10{\rm{ kgm}}{{\rm{s}}^{ - 1}}\] for \[{P_i}\] in equation (1), we get:
\[
{P_f} = 23.625{\rm{ kgm}}{{\rm{s}}^{ - 1}} + 10{\rm{ kgm}}{{\rm{s}}^{ - 1}}\\
\Rightarrow{P_f} = 33.625{\rm{ kgm}}{{\rm{s}}^{ - 1}}
\]
Let us write the expression for the final momentum of the body, which is equal to the product of its mass and final velocity.
\[{P_f} = m{V_f}\]
Here \[{V_f}\] is the final velocity of the body.
On substituting \[33.625{\rm{ kgm}}{{\rm{s}}^{ - 1}}\] for \[{P_f}\] and \[2{\rm{ kg}}\] for m in the above expression, we get:
\[
33.625{\rm{ kgm}}{{\rm{s}}^{ - 1}} = \left( {2{\rm{ kg}}} \right){V_f}\\
\therefore{V_f} = 16.812{\rm{ m}}{{\rm{s}}^{ - 1}}
\]
Therefore, the final velocity of the given body is \[16.812{\rm{ m}}{{\rm{s}}^{ - 1}}\] , and all options are incorrect.

Note: We have to be extra careful while calculating the area of the given curve because there are many separate areas involved, so chances of mistakes are more. We can also remember the unit of momentum, which is \[{\rm{kgm}}{{\rm{s}}^{ - 1}}\].