
A body of mass 0.1 kg when rotated in a circular path of diameter 1.0 m in a frictionless horizontal plane by means of a string, makes 10 revolutions in 31.4 seconds. The centripetal force acting on the body will be.
A. 0.2 N
B. 0.1 N
C. 2 N
D. 1 N
Answer
604.8k+ views
Hint: In this question we start with the basic formula for the centripetal force that is \[{F_C} = mr{\omega ^2}\]. But for this we need to find $\omega $ in rad/sec using the formula $\omega = \dfrac{{rad}}{{\text{second}}} = \dfrac{N}{{60}}2\pi $ but before that we need to convert revolution/sec to revolution/minute. Then solve for centripetal force ${F_C}$.
Complete Step-by-Step solution:
We know that a centripetal force is a force that develops when an object is moving in a circular path. Its direction is always perpendicular to the motion of the body and towards the fixed point of the instantaneous center of the circular path. This can be seen in figure 1
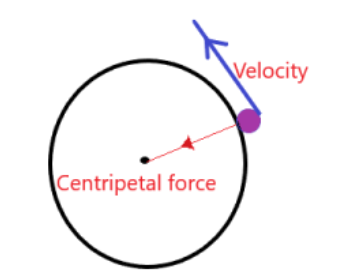
Now the formula for the centripetal force is given by
\[{F_C} = mr{\omega ^2}\]-------------------------------------- (1)
Where ${F_C}$ is the centripetal force in N.
$m$ is the mass of the object which is given as 0.1 Kg.
$r$ is the radius of the circular path in $\dfrac{1}{2} = 0.5m$ m because diameter is given 1 m
$\omega = \dfrac{v}{r}$ is the angular velocity in rad/sec.
We can also write equation (1) as:
\[{F_C} = {\dfrac{{mv}}{r}^2}\]---------------------------------------- (2)
First, we need to find the angular velocity for that we were given 10 revolutions in 31.4 seconds but we know that:
$\omega = \dfrac{{rad}}{{\text{second}}} = \dfrac{N}{{60}}2\pi $------------------ (3)
So first we need to find N that is the speed in revolution/minute that is rpm.
$ \Rightarrow 31.4\text{second} = 10revolution$
$ \Rightarrow 1\text{second} = \dfrac{{10}}{{31.4}}revolution$
$ \Rightarrow 1\text{minute} = \dfrac{{10}}{{31.4}} \times 60revolution$
$ \Rightarrow N = \dfrac{{600}}{{31.4}}rpm$
Now substituting speed in rpm in equation number (3). We get
$ \Rightarrow \omega = \dfrac{{600}}{{31.4 \times 60}} \times 2\pi rad/\sec $
$ \Rightarrow \omega = \dfrac{{{6}{0}{0}}}{{1{0}{\pi } \times {6}{0}}} \times 2{\pi }rad/\sec $
$ \Rightarrow \omega = 2rad/\sec $
Now substituting the value of $\omega $,$m$ and $r$ in the equation (1). We will get the value of centripetal force is:
\[{F_C} = mr{\omega ^2} = \left( {0.1} \right) \times \left( {0.5} \right) \times {2^2} = 0.2N\]
So the required centripetal force is 0.2N that is acting on the given body
So the correct option is A.
Note: In these types of questions we need to know about different types of force that is centripetal force, centrifugal force, gravitational force, and force due acceleration. We also need to know about the expression for finding the above mentioned force. Take care of unit conversion when needed.
Complete Step-by-Step solution:
We know that a centripetal force is a force that develops when an object is moving in a circular path. Its direction is always perpendicular to the motion of the body and towards the fixed point of the instantaneous center of the circular path. This can be seen in figure 1

Figure 1
Now the formula for the centripetal force is given by
\[{F_C} = mr{\omega ^2}\]-------------------------------------- (1)
Where ${F_C}$ is the centripetal force in N.
$m$ is the mass of the object which is given as 0.1 Kg.
$r$ is the radius of the circular path in $\dfrac{1}{2} = 0.5m$ m because diameter is given 1 m
$\omega = \dfrac{v}{r}$ is the angular velocity in rad/sec.
We can also write equation (1) as:
\[{F_C} = {\dfrac{{mv}}{r}^2}\]---------------------------------------- (2)
First, we need to find the angular velocity for that we were given 10 revolutions in 31.4 seconds but we know that:
$\omega = \dfrac{{rad}}{{\text{second}}} = \dfrac{N}{{60}}2\pi $------------------ (3)
So first we need to find N that is the speed in revolution/minute that is rpm.
$ \Rightarrow 31.4\text{second} = 10revolution$
$ \Rightarrow 1\text{second} = \dfrac{{10}}{{31.4}}revolution$
$ \Rightarrow 1\text{minute} = \dfrac{{10}}{{31.4}} \times 60revolution$
$ \Rightarrow N = \dfrac{{600}}{{31.4}}rpm$
Now substituting speed in rpm in equation number (3). We get
$ \Rightarrow \omega = \dfrac{{600}}{{31.4 \times 60}} \times 2\pi rad/\sec $
$ \Rightarrow \omega = \dfrac{{{6}{0}{0}}}{{1{0}{\pi } \times {6}{0}}} \times 2{\pi }rad/\sec $
$ \Rightarrow \omega = 2rad/\sec $
Now substituting the value of $\omega $,$m$ and $r$ in the equation (1). We will get the value of centripetal force is:
\[{F_C} = mr{\omega ^2} = \left( {0.1} \right) \times \left( {0.5} \right) \times {2^2} = 0.2N\]
So the required centripetal force is 0.2N that is acting on the given body
So the correct option is A.
Note: In these types of questions we need to know about different types of force that is centripetal force, centrifugal force, gravitational force, and force due acceleration. We also need to know about the expression for finding the above mentioned force. Take care of unit conversion when needed.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




