Question

A body is moving with a velocity $72\;kmh^{-1}$ on a rough horizontal surface of coefficient of friction 0.5. If the acceleration due to gravity is $10\;ms^{-2}$, find the distance it covers before it comes to rest.
A.10m
B.20m
C.30m
D.40m

Answer 1

Hint: First calculate the effective acceleration of the body while accounting for the frictional retardation offered to the motion of the body. Then, use a kinematic equation relating velocity, acceleration and distance travelled to ultimately arrive at the distance that the body covers before retarding to a halt. Note that the frictional acceleration (retardation) will be in a direction opposite to the motion of the body, so assign directional signs accordingly.

Formula Used:
Frictional force $F_{frictional} = \mu N$
Kinematic equation of motion $v^2 -u^2 =2as$

Complete answer:
We are given that the initial velocity of the body is $u = 72\;kmh^{-1} = 72 \times \dfrac{10^3}{3600} = 20\;ms^{-1}$.
The coefficient of friction $\mu = 0.5$. This means that the acceleration of the body and consequently the force acting on it is impeded by a frictional force.

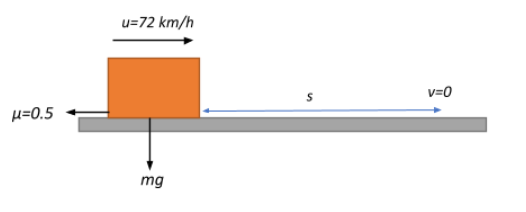
The magnitude of the frictional force is given as $F_{frictional} = \mu N$, where N is the normal reaction force on the body, equivalent to the gravitational force in magnitude.
$\Rightarrow F_{frictional} = -\mu mg \Rightarrow a_{frictional} = -\mu g = -0.5 \times 10 = -5\;ms^{-2}$ where the negative sign indicates that it acts in a direction opposite to the motion of the body.
Now that we have the effective acceleration of the block as $a = -5\;ms^{-2}$, we can determine the distance it travels before coming to a complete stop $v=0$ by using a kinematic equation of motion:
$v^2 – u^2 = 2as \Rightarrow s = \dfrac{v^2-u^2}{2a}$
$\Rightarrow s = \dfrac{0-20^2}{2\times -5} = \dfrac{-400}{-10} = 40\;m$

Therefore, the correct option would be D. 40m

Note:
Note that though we termed the impedance offered to the body by the coefficient friction as an effective acceleration, it is technically a retardation that brings out the stopping of the body, without which the body would continue to execute its motion incessantly. Thus, always remember to assign proper signs to acceleration and retardation components to avoid any conceptual confusion that may lead to numerical inconsistencies.