
A bob hangs from a rigid support by an inextensible string of length
A.
B.
C.
D.

Answer
464.7k+ views
Hint: We need to use the principle of conservation of energy between the highest point and the lowest point. For calculation of potential energy, find the vertical distance of the bob at the highest position from the lowest position.
Formula used:
In this solution we will be using the following formulae;
Complete answer:
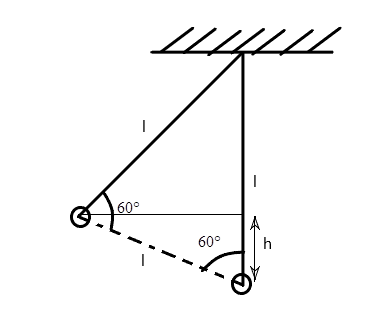
First, we see from diagram, that the height of the bob above the lowest point can be given by
Now, using the lowest point as the reference point, the potential energy of the bob can be found using the formula
Hence,
Now, according to the principle of conservation of energy, all the potential at the highest point will be converted to kinetic energy at the lowest point. The kinetic energy is
Hence,
Hence, by making
Hence, the correct option is A.
Note:
For clarity, note that the point of reference is not essential to the calculation of the velocity, any point can be used as a reference point. The potential energy is always based on some point of reference.
Formula used:
In this solution we will be using the following formulae;
Complete answer:

First, we see from diagram, that the height of the bob above the lowest point can be given by
Now, using the lowest point as the reference point, the potential energy of the bob can be found using the formula
Hence,
Now, according to the principle of conservation of energy, all the potential at the highest point will be converted to kinetic energy at the lowest point. The kinetic energy is
Hence,
Hence, by making
Hence, the correct option is A.
Note:
For clarity, note that the point of reference is not essential to the calculation of the velocity, any point can be used as a reference point. The potential energy is always based on some point of reference.
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Trending doubts
Difference Between Prokaryotic Cells and Eukaryotic Cells

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Net gain of ATP in glycolysis a 6 b 2 c 4 d 8 class 11 biology CBSE

Give two reasons to justify a Water at room temperature class 11 chemistry CBSE




