Question

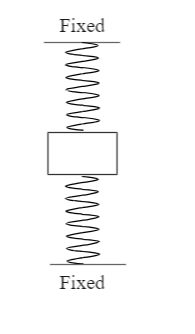
A block tied between two springs is in equilibrium. If the upper spring is cut then the acceleration of the block just after the cut is $6m/{s^2}$ downwards. Now, if instead of the upper spring, lower spring is cut then the magnitude of acceleration of the block just after the cut will be? (Take $g = 10m/{s^2}$)

(A) $16m/{s^2}$
(B) $4m/{s^2}$
(C) Cannot be determined
(D) None of these

Answer 1

Hint:
A body stays in equilibrium only when all the forces acting on it are balanced in all the directions. As and when the objects responsible for exerting a force on the mass are removed or added, the total force experienced by the body changes.
Formula used: $F = ma$, where F is the force acting on the body of mass m moving with acceleration a.

Complete step by step answer:
We are provided with a mass that stays in equilibrium with the help of two springs that are attached to it. When either of the springs will be removed, the natural balance of the mass will break and it will start moving in a direction depending on the total force exerted on it.
Let us assume the following forces due to the two springs acting in the upwards direction:
Force due to upper spring ${F_1}$
Force due to lower spring ${F_2}$
Mass of the block is m
We know that the force due to the weight of the object will be acting downwards as mg. So, by force balance we can write:
$\Rightarrow {F_1} + {F_2} = mg = 10m$ [Eq. 1]
When the upper spring is removed, only ${F_2}$ and mg will be acting on the block to produce a net force with acceleration a, which is given in the downward direction as:
$\Rightarrow mg - {F_2} = ma$
We know this acceleration is $6m/{s^2}$. Hence,
$\Rightarrow 10m - {F_2} = 6m$
$\Rightarrow {F_2} = 10m - 6m = 4m$
From Eq. 1, we get:
$\Rightarrow {F_1} = 10m - {F_2} = 6m$
Now, when the lower spring is cut, let us assume acceleration a acts downwards on it creating a force as:
$\Rightarrow mg - {F_1} = ma$
$\Rightarrow 10m - 6m = ma$
Hence, the acceleration will be $4m/{s^2}$ downwards, that is option (B).

Note:
The force exerted due to a spring is the restoring force. This is because as the spring is stretched or contracted along its length from the mean or equilibrium position, the restoring force tries to push it back to the original position. That way these can be used to balance objects.