Question

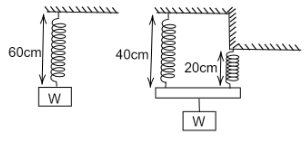
A block of weight W produces an extension of $ 9cm $ when it is hung by an elastic spring of length $ 60cm $ and is in equilibrium. The spring is cut into two parts, one of length $ 40cm $ and the other of length $ 20cm $ . The same load $ W $ hangs in equilibrium supported by both parts as shown in the figure. The extension now is:

Answer 1

Hint : The two cut parts of the spring are assumed to be two different springs. In first case they are assumed to be connected in series and in next they are connected in parallel. We can solve for the value of these constants and then calculate the extension produced when they are connected in parallel.

Formula used:
 $\Rightarrow F = kx $
In series connection ,
 $\Rightarrow \dfrac{1}{{{k_{eff}}}} = \dfrac{1}{{{k_1}}} + \dfrac{1}{{{k_2}}} $
In parallel connection,
 $\Rightarrow {k_{eff}} = {k_1} + {k_2} $
Where $ {k_{eff}} $ is the effective spring constant, $ {k_1} $ and $ {k_2} $ are the individual spring constants, $ x $ is the extension. $ F $ is the restoring force.

Complete step by step answer
It is given in the question that,
The weight of the block is $ W $ .
Extension produced in the spring when $ W $ is connected is $ 9cm $ .
We know that, force in a spring is given by,
 $\Rightarrow F = kx $
Where $ k $ is the spring constant.
And $ x $ is the extension produced in it.
Let the spring constant in the first case be $ {k_A} $
Comparing this with the spring in question,
 $\Rightarrow W = {k_A} \times 9 $
 $\Rightarrow {k_A} = \dfrac{W}{9} $
This relation shows that $ k $ is inversely proportional to the extension.
In the second case the spring is cut into two parts, let their spring constants be $ {k_1} $ and $ {k_2} $ .
Since $ k $ is inversely proportional to the length,
 $\Rightarrow \dfrac{{{k_1}}}{{{k_2}}} = \dfrac{{{l_2}}}{{{l_1}}} $
It is given that, $ {l_1} = 40 $ and $ {l_2} = 20 $ cm.
 $\Rightarrow \dfrac{{{k_1}}}{{{k_2}}} = \dfrac{{20}}{{40}} $
On simplifying this we obtain,
 $\Rightarrow 2{k_1} = {k_2} $
For the first case it can be assumed that springs were connected in series (end to end connection),
Adding $ {k_1} $ and $ {k_2} $ as per series connection,
 $\Rightarrow \dfrac{1}{{{k_A}}} = \dfrac{1}{{{k_1}}} + \dfrac{1}{{{k_2}}} $
Or, $ {k_A} = \dfrac{{{k_1}{k_2}}}{{{k_1} + {k_2}}} $
Substituting, $ 2{k_1} = {k_2} $ ,
 $\Rightarrow {k_A} = \dfrac{{2{k_1}^2}}{{{k_1} + 2{k_1}}} = \dfrac{{2{k_1}}}{3} $
 $\Rightarrow {k_1} = \dfrac{{3{k_A}}}{2} $
Similarly,
 $\Rightarrow {k_2} = 2 \times \dfrac{3}{2}{k_A} $
 $\Rightarrow {k_2} = 3{k_A} $
The effective spring constant when both springs are connected in parallel is given by,
 $\Rightarrow {k_B} = {k_1} + {k_2} $
In terms of $ {k_A} $ ,
 $\Rightarrow {k_B} = \left( {\dfrac{3}{2} + 3} \right){k_A} $
 $\Rightarrow {k_B} = \dfrac{9}{2}{k_A} $
For extension,
 $\Rightarrow W = {k_B}x $
On substituting the value of $ W $ and $ {k_B} $ we get,
 $\Rightarrow 9{k_A} = \dfrac{9}{2}{k_A}x $
 $\therefore x = 2 $
Therefore the extension produced in the second case is $ 2cm $ .

Note
When two or more springs are connected in parallel the effective spring constant is more than the highest value of spring constant, whereas when the springs are connected in series, the effective spring constant is less than the least value of spring constant.