Question

A block of silver of mass of 4kg hanging from a string is immersed in liquid of relative density 0.72. If relative density of silver is 10, then tension in the string will be [Take $g=10m{{s}^{-2}}$]
a) 37.12 N
b) 42.21 N
c) 73.7 N
d) 21.13 N

Answer 1

Hint: The relative density of the substance is defined as the ratio of density of the substance to that of density of water. The string is assumed to be massless. Therefore the tension in the string will due to the net force acting on the silver block downwards.
Formula used:
${{F}_{B}}={{\rho }_{L}}gV$
${{F}_{G}}=mg$

Complete answer:

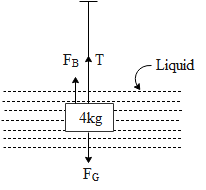
Let us say there is uniform tension ‘T’ in the string. From the above diagram we can see that the buoyant force (${{F}_{B}}$ )acts in the upward direction while the while the gravitational force (${{F}_{G}}$) acts in the downward direction. The net force on the block is zero i.e. there is no relative motion of the block. Hence from the above free body diagram of the silver block, the equation for net force on the body is given by,
${{F}_{G}}-{{F}_{B}}-T=0$
The gravitational force on a body of mass ‘m’ acceleration at ‘g’ is given by,
${{F}_{G}}=mg$
Further let us say a body of volume ‘V’ is completely immersed in a liquid of density ${{\rho }_{L}}$ . Therefore the buoyant force on the body is given by,
${{F}_{B}}={{\rho }_{L}}gV$ . Hence the equation of motion for the silver block is,
$\begin{align}
  & mg-{{\rho }_{L}}gV-T=0 \\
 & \therefore T=mg-{{\rho }_{L}}gV....(1) \\
\end{align}$
Let us say the density of silver be${{\rho }_{s}}$ , density of the liquid be ${{\rho }_{L}}$ and density of water be ${{\rho }_{w}}$ . Therefore the relative density of silver is given by,
${{\rho }_{s/w}}=\dfrac{{{\rho }_{s}}}{{{\rho }_{w}}}.....(2)$ and that of the liquid is given by,
${{\rho }_{L/w}}=\dfrac{{{\rho }_{L}}}{{{\rho }_{w}}}....(3)$
The relative density of silver and the liquid is given to us. Hence dividing equation 3 by 2 we get,
$\begin{align}
  & \dfrac{{{\rho }_{L/w}}}{{{\rho }_{s/w}}}=\dfrac{\dfrac{{{\rho }_{L}}}{{{\rho }_{w}}}}{\dfrac{{{\rho }_{s}}}{{{\rho }_{w}}}} \\
 & \Rightarrow \dfrac{0.72}{10}=\dfrac{{{\rho }_{L}}}{{{\rho }_{s}}} \\
 & \therefore \dfrac{{{\rho }_{L}}}{{{\rho }_{s}}}=0.072 \\
\end{align}$
The tension in the string from equation 1 is numerically equal to,
$\begin{align}
  & T=mg-{{\rho }_{L}}gV \\
 & \Rightarrow T=m\left( g-\dfrac{{{\rho }_{L}}g}{\dfrac{m}{V}} \right) \\
 & \because \dfrac{m}{V}={{\rho }_{s}} \\
 & \Rightarrow T=4kg\left( 10-\dfrac{{{\rho }_{L}}(10)}{{{\rho }_{s}}} \right) \\
 & \because \dfrac{{{\rho }_{L}}}{{{\rho }_{s}}}=0.072 \\
 & \Rightarrow T=4\left[ 10-0.072(10) \right] \\
 & \Rightarrow T=4\left[ 9.28 \right]N \\
 & \therefore T=37.12N \\
\end{align}$

Therefore the correct answer of the above question is option a.

Note:
The density of any substance is defined as the mass per unit volume of that substance. The string in the question is assumed to be mass less as well we have not considered the viscous force. If we account those factors as well the above equations do not hold valid.