Question

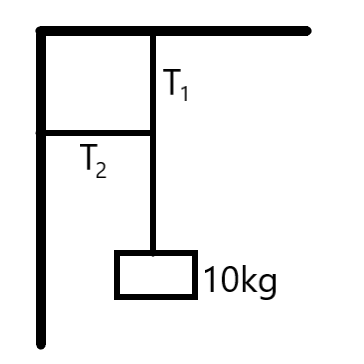
A block of mass $m=10kg$ is suspended with the help of three strings as shown in the figure. Find the tensions ${{T}_{1}}$ and ${{T}_{2}}$
$\begin{align}
  & A)100N,0N \\
 & B)0N,100N \\
 & C)50N,50N \\
 & D)60N,80N \\
\end{align}$

Answer 1

Hint: Tension on a body refers to the pulling force experienced by the body due to an attached string, cable or chain, from a hard surface like wall. Tensions ${{T}_{1}}$ and ${{T}_{2}}$ in the given figure are perpendicular to each other. When the given weight is balanced with the help of three strings, the system is in equilibrium. The sum of forces along the x-axis as well as the sum of forces along the y-axis at the point of connection of three strings (equilibrium point) is equal to zero.
Formula used:
$1)W=mg$
$2)\sum{Fx}=\sum{Fy}=0$

Complete answer:
We are provided with a block of mass $m=10kg$, suspended with the help of three strings, as shown in the following figure. We are required to find tensions ${{T}_{1}}$ and ${{T}_{2}}$.

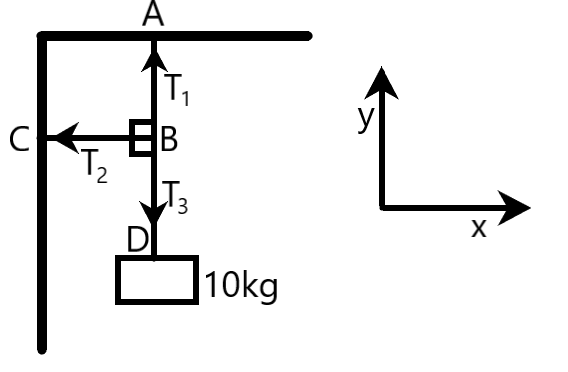
Firstly, let us name the points as well as the strings in the given figure.
Clearly, from the modified figure, we have
$AB$- first string which experiences tension ${{T}_{1}}$
$CB$- second string which experiences tension ${{T}_{2}}$
$DB$- third string which experiences tension ${{T}_{3}}$ (assumed), due to the block of mass $m=10kg$
Now, we know that tension on a body is defined as the pulling force experienced by the body due to an attached string, cable or chain from a hard surface like wall. Therefore, tension ${{T}_{1}}$ in the given figure acts in direction $BA$because string $AB$ is attached to the wall at the top. Similarly, tension ${{T}_{2}}$ acts in the direction $BC$ because string $CB$ is attached to the wall on the left side. Tension ${{T}_{3}}$ acts in the direction $BD$ because of the weight of the given mass.
Clearly, all the tensions ${{T}_{1}},{{T}_{2}}$ and ${{T}_{3}}$ are acting perpendicular to each other, as shown in the figure.
If $W$represents the weight of given mass, then, $W$ is given by
$W=mg=10kg\times 10m{{s}^{-2}}=100kgm{{s}^{-2}}=100N$
where
$m=10kg$ is the mass of the block, as provided
$g=10m{{s}^{-2}}$, is the acceleration due to gravity
Let this be equation 1.
Now, when the given mass is balanced with the help of three strings, the system is said to be in equilibrium. At equilibrium, we can say that the sum of forces acting along the x-axis as well as the sum of forces acting along the y-axis is equal to zero. Clearly, at the equilibrium position $B$, we have
$\sum{Fx}=\sum{Fy}=0$
Let this be equation 2.
Now, let us determine the forces at point $B$, along the x-axis.
Clearly, the only force acting along the x-axis is the tension ${{T}_{2}}$along $BC$. Therefore, using equation 2, we can write
\[\sum{Fx}=0\Rightarrow {{T}_{2}}=0\]
Let this be equation 3.
Now, let us move on to determine all the forces at point $B$, along the x-axis.
Clearly, there are two forces acting along the y-axis in opposite directions. They are ${{T}_{1}}$ along $BA$ and ${{T}_{3}}$ along $BD$ . Therefore, using equation 2, we can write
$\sum{Fy=0\Rightarrow {{T}_{1}}-{{T}_{3}}=0}$
Let this be equation 4.
Now, we know that tension acting along $BD$$({{T}_{3}})$ is equal to the weight of the given block, in the opposite direction. Therefore, we can write
${{T}_{3}}=W=mg=100kgm{{s}^{-2}}=100N$
Let this be equation 5.
Substituting equation 5 in equation 4, we have
\[{{T}_{1}}-{{T}_{3}}=0\Rightarrow {{T}_{1}}-100N=0\Rightarrow {{T}_{1}}=100N\]
Let this be equation 6.
Therefore, from equation 3 and equation 6, tensions ${{T}_{1}}$ and ${{T}_{2}}$ are equal to $100N$and $0N$, respectively.

So, the correct answer is “Option A”.

Note:
Students can also relate this problem to Lami’s theorem, which talks about the magnitudes of three coplanar, concurrent and non-collinear vectors, which balance an object in static equilibrium.
According to Lami’s theorem,
$\dfrac{A}{\sin \alpha }=\dfrac{B}{\sin \beta }=\dfrac{C}{\sin \gamma }$
where
$A,B,C$ are the magnitudes of forces which keep an object balanced in static equilibrium
$\alpha ,\beta ,\gamma $ are the angles directly opposite to the corresponding forces given above.
The method used in the above solution is easier than determining the tensions using Lami’s theorem.