
A block of mass $ m $ lying on a smooth horizontal surface is attached to a spring of spring constant $ k $ . The other end of the end is fixed, as shown in the figure. The block is initially at rest in its equilibrium position. If now the block is pulled with a constant force $ F, $ the maximum speed of the block is:

(A) $ \dfrac{{\pi F}}{{\sqrt {mk} }} $
(B) $ \dfrac{{2F}}{{\sqrt {mk} }} $
(C) $ \dfrac{F}{{\sqrt {mk} }} $
(D) $ \dfrac{F}{{\pi \sqrt {mk} }} $

Answer
555.3k+ views
Hint
To solve this question, firstly we have to find the maximum extension of the spring. From there we can get the maximum potential energy of the block, which can be equated to the maximum kinetic energy to get the maximum speed.
Formula Used:
The formula used to solve this question is given by:
$ \Rightarrow U = \dfrac{1}{2}k{x^2} $ where $ U $ is the potential energy of a spring of spring constant $ k $ having extension $ x $
$ \Rightarrow K = \dfrac{1}{2}m{v^2} $ Where is $ K $ the kinetic energy of a particle of mass $ m $ moving with speed $ v $
Complete step by step answer
The situation is shown in the below diagram
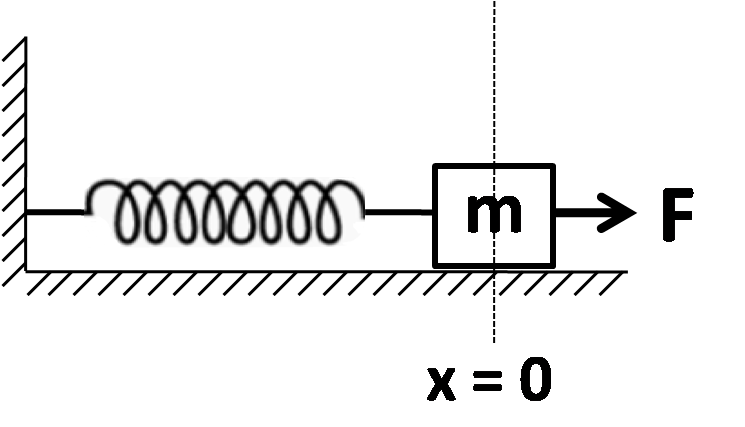
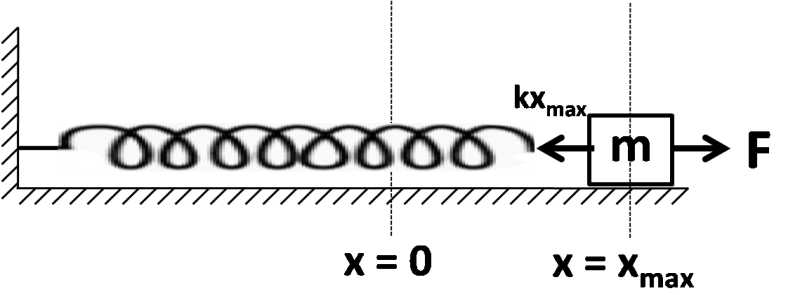
We fix the origin at the initial position of the block. Now, on the application of the force $ F, $ we have the maximum extension $ {x_{\max }} $ , which can be found by putting net force equal to zero at the maximum extension.
So, we have from the equilibrium of the block
$ F = k{x_{\max }} $
Or, $ {x_{\max }} = \dfrac{F}{k} $ (1)
Now, we know that the potential energy of a stretched spring is given by
$\Rightarrow U = \dfrac{1}{2}k{x^2} $
So, the maximum potential energy of the stretched spring is equal to
$\Rightarrow {U_{\max }} = \dfrac{1}{2}k{x_{\max }}^2 $ (2)
We also know that the kinetic energy of an object is given by
$\Rightarrow K = \dfrac{1}{2}m{v^2} $
So, the maximum kinetic energy is
$\Rightarrow {K_{\max }} = \dfrac{1}{2}m{v_{\max }}^2 $ (3)
Since there is no friction, the total energy of the block remains constant. Also, we know that when the kinetic energy of the block is maximum, its potential energy is zero and vice-versa.
Therefore we can say that
$\Rightarrow {K_{\max }} = {U_{\max }} $
From (2) and (3) we have
$\Rightarrow \dfrac{1}{2}m{v_{\max }}^2 = \dfrac{1}{2}k{x_{\max }}^2 $
Multiplying both sides by $ \dfrac{2}{m} $
$\Rightarrow {v_{\max }}^2 = \dfrac{2}{m} \times \dfrac{1}{2}k{x_{\max }}^2 $
$\Rightarrow {v_{\max }}^2 = \dfrac{k}{m}{x_{\max }}^2 $
Substituting the value of $ {x_{\max }} $ from (1), we get
$\Rightarrow {v_{\max }}^2 = \dfrac{k}{m}{\left( {\dfrac{F}{k}} \right)^2} $
$\Rightarrow {v_{\max }}^2 = {\dfrac{F}{{mk}}^2} $
Finally, taking square root we get
$\Rightarrow {v_{\max }} = \dfrac{F}{{\sqrt {mk} }} $
Therefore, the maximum speed of the block is equal to $ \dfrac{F}{{\sqrt {mk} }} $
Hence, the correct answer is option (C), $ \dfrac{F}{{\sqrt {mk} }} $ .
Note
The same question can also be solved using the work-energy theorem. We just need to find the work done by the constant force and the spring force, which is to be equated with the change in kinetic energy, at the extreme position. But the first step to solve these types of questions, by any method is to find out the maximum extension of the spring.
To solve this question, firstly we have to find the maximum extension of the spring. From there we can get the maximum potential energy of the block, which can be equated to the maximum kinetic energy to get the maximum speed.
Formula Used:
The formula used to solve this question is given by:
$ \Rightarrow U = \dfrac{1}{2}k{x^2} $ where $ U $ is the potential energy of a spring of spring constant $ k $ having extension $ x $
$ \Rightarrow K = \dfrac{1}{2}m{v^2} $ Where is $ K $ the kinetic energy of a particle of mass $ m $ moving with speed $ v $
Complete step by step answer
The situation is shown in the below diagram


We fix the origin at the initial position of the block. Now, on the application of the force $ F, $ we have the maximum extension $ {x_{\max }} $ , which can be found by putting net force equal to zero at the maximum extension.
So, we have from the equilibrium of the block
$ F = k{x_{\max }} $
Or, $ {x_{\max }} = \dfrac{F}{k} $ (1)
Now, we know that the potential energy of a stretched spring is given by
$\Rightarrow U = \dfrac{1}{2}k{x^2} $
So, the maximum potential energy of the stretched spring is equal to
$\Rightarrow {U_{\max }} = \dfrac{1}{2}k{x_{\max }}^2 $ (2)
We also know that the kinetic energy of an object is given by
$\Rightarrow K = \dfrac{1}{2}m{v^2} $
So, the maximum kinetic energy is
$\Rightarrow {K_{\max }} = \dfrac{1}{2}m{v_{\max }}^2 $ (3)
Since there is no friction, the total energy of the block remains constant. Also, we know that when the kinetic energy of the block is maximum, its potential energy is zero and vice-versa.
Therefore we can say that
$\Rightarrow {K_{\max }} = {U_{\max }} $
From (2) and (3) we have
$\Rightarrow \dfrac{1}{2}m{v_{\max }}^2 = \dfrac{1}{2}k{x_{\max }}^2 $
Multiplying both sides by $ \dfrac{2}{m} $
$\Rightarrow {v_{\max }}^2 = \dfrac{2}{m} \times \dfrac{1}{2}k{x_{\max }}^2 $
$\Rightarrow {v_{\max }}^2 = \dfrac{k}{m}{x_{\max }}^2 $
Substituting the value of $ {x_{\max }} $ from (1), we get
$\Rightarrow {v_{\max }}^2 = \dfrac{k}{m}{\left( {\dfrac{F}{k}} \right)^2} $
$\Rightarrow {v_{\max }}^2 = {\dfrac{F}{{mk}}^2} $
Finally, taking square root we get
$\Rightarrow {v_{\max }} = \dfrac{F}{{\sqrt {mk} }} $
Therefore, the maximum speed of the block is equal to $ \dfrac{F}{{\sqrt {mk} }} $
Hence, the correct answer is option (C), $ \dfrac{F}{{\sqrt {mk} }} $ .
Note
The same question can also be solved using the work-energy theorem. We just need to find the work done by the constant force and the spring force, which is to be equated with the change in kinetic energy, at the extreme position. But the first step to solve these types of questions, by any method is to find out the maximum extension of the spring.
Recently Updated Pages
Master Class 11 Chemistry: Engaging Questions & Answers for Success

Why are manures considered better than fertilizers class 11 biology CBSE

Find the coordinates of the midpoint of the line segment class 11 maths CBSE

Distinguish between static friction limiting friction class 11 physics CBSE

The Chairman of the constituent Assembly was A Jawaharlal class 11 social science CBSE

The first National Commission on Labour NCL submitted class 11 social science CBSE

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




