Question

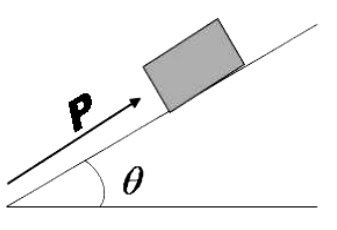
A block of mass m is on an inclined plane of angle $\theta $. The coefficient of friction between the block and the plane is $\mu $ and $\tan \theta > \mu $. The block is held stationary by applying a force P parallel to the plane. The direction of force pointing up the plane is taken to be positive. As P is varied from ${{P}_{1}}=mg\left( \sin \theta -\mu \cos \theta \right)$ to ${{P}_{2}}=mg\left( \sin \theta +\mu \cos \theta \right)$, the frictional force f versus P graph will look like

A.

B.

C.

D.

Answer 1

Hint: We know that when force P that was used to keep the block stationary on the plane is increased the block will move up the plane. You could make free body diagrams for both cases and then compare. Also, you could clearly understand the variation of f with P and hence find the correct plot representing the same.

Complete answer:
In the question we are given a block of mass m kept on an incline plane of angle $\theta $ and the coefficient of friction between the lock and the plane is given as$\theta $. The block is being applied with a force P parallel to the plane to keep it from sliding. Now P is varied. We have to identify which among the given graphs correctly represent the frictional force f versus P graph.
When the block is kept stationary by P, the free body diagram could be given by,

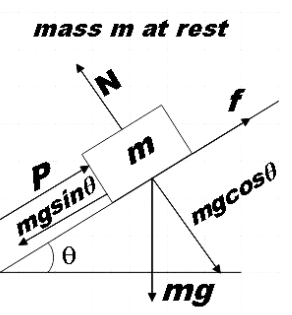
Now we could balance all the forces.
Perpendicular to plane we have,
$N=mg\cos \theta $………………. (1)
Parallel to plane we have,
${{P}_{1}}+f=mg\sin \theta $
$\Rightarrow f=mg\sin \theta -{{P}_{1}}$ ……………………. (2)
Now when we increase P, the block will move up the incline plane from rest and the frictional force which normally opposes the relative motion between surfaces changes direction. Therefore the FBD now becomes,

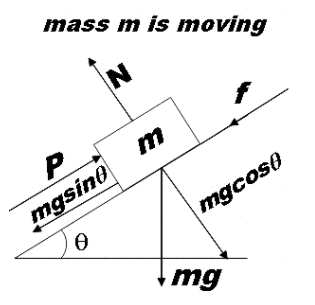
Here,
$f={{P}_{2}}-mg\sin \theta $ …………………………… (3)
In comparison with (2) we see that frictional force has changed direction.
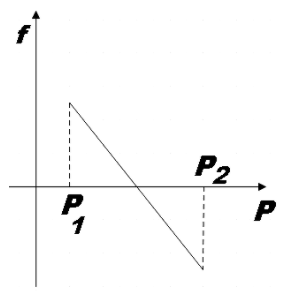
So for force ${{P}_{2}}$ we have the same magnitude for frictional force as ${{P}_{1}}$ but will be negative as we are given that the direction of force pointing up the plane is taken to be positive. So the graph that aptly represents the variation of f with P will be,

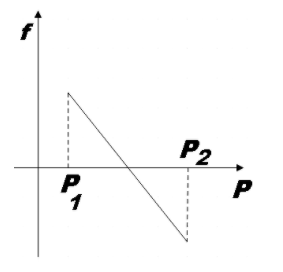
Hence, option A is the right answer.

Note:
We know that the frictional force is given by,
$f=\mu N$
Where, N is the normal force. We could substitute the normal force from (1) to get,
$f=\mu mg\cos \theta $
Also, by substituting this in (2) and (3), we get the same ${{P}_{1}}$ and ${{P}_{2}}$ as given in the question.