
A block of mass


Answer
495k+ views
Hint: Then the frequency of the small oscillation will be found by taking the product of
Complete answer:
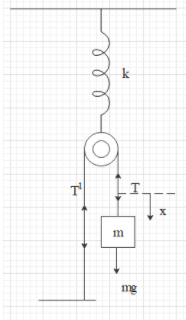
Suppose the block will be depressed by
For the block we can mention that,
In the case of the pulley, we can write that,
Where
The angular acceleration of the pulley can be found by taking the ratio mentioned as,
And also we can write that,
From the equations 1, 2, 3 and 4, we can write that,
Then the frequency of the small oscillation will be found by taking the product of
Therefore the frequency of the oscillation has been calculated.
Note:
Frequency of the oscillation can be defined as the number of oscillations completed in a unit period of time. The frequency is found to be the reciprocal of the time period. The unit of frequency has been found to be hertz.
Complete answer:

Suppose the block will be depressed by
For the block we can mention that,
In the case of the pulley, we can write that,
Where
The angular acceleration of the pulley can be found by taking the ratio mentioned as,
And also we can write that,
From the equations 1, 2, 3 and 4, we can write that,
Then the frequency of the small oscillation will be found by taking the product of
Therefore the frequency of the oscillation has been calculated.
Note:
Frequency of the oscillation can be defined as the number of oscillations completed in a unit period of time. The frequency is found to be the reciprocal of the time period. The unit of frequency has been found to be hertz.
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Trending doubts
1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

How do I get the molar mass of urea class 11 chemistry CBSE

How do I convert ms to kmh Give an example class 11 physics CBSE

Where can free central placentation be seen class 11 biology CBSE

What is the molecular weight of NaOH class 11 chemistry CBSE

What is 1s 2s 2p 3s 3p class 11 chemistry CBSE




