Question

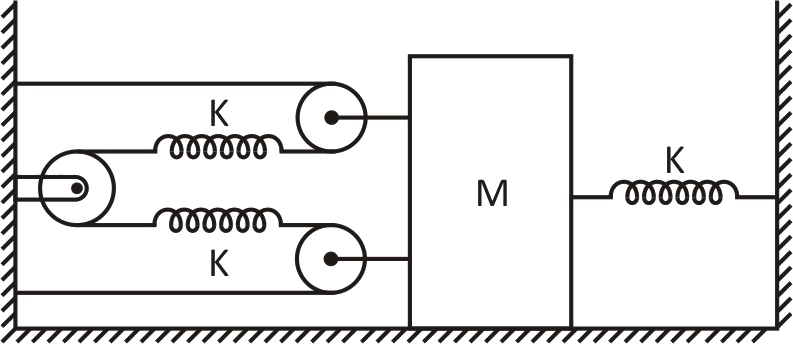
A block of mass \[M\] is attached with the springs as shown. If the block is slightly displaced, the time speed of \[SHM\] for the block shown in the figure will be

(A) \[2\pi \sqrt {\dfrac{m}{{9K}}} \]
(B) \[2\pi \sqrt {\dfrac{m}{K}} \]
(C) \[\dfrac{{4\pi }}{3}\sqrt {\dfrac{m}{K}} \]
(D) \[\pi \sqrt {\dfrac{m}{{2K}}} \]

Answer 1

Hint: SHM is known for simple harmonic motion. Simple harmonic motion is defined as a motion in which the restoring force is directly proportional to displacement of the object from its mean position.

Complete step by step answer:
Given that, the mass\[M\] is attached to the springs and the block is slightly displaced. Let \[{T_1}\] and \[{T_2}\] be restoring forces.
As shown in diagram \[A\] , \[B\] and \[C\] are springs.
Let block \[M\] moved distance \[x\] to the left side
Then extension in spring \[A\] = \[x\]
Compression in \[B\] and \[C\] =\[0\]
Let \[{T_2}\] be restoring force to left side =\[Kx\] ∴ \[K\] is force constant
Then, \[{T_1}\] = \[\dfrac{{2\pi }}{2}\sqrt {\dfrac{m}{K}} \] = \[\pi \sqrt {\dfrac{m}{K}} \]
When \[M\] moved distance \[y\] to the right side.
Then extension in both springs \[B\] and \[C\] =\[2\] \[y\]
Compression in \[A\] = \[y\]
\[{T_1}\] is restoring force to right = \[2Ky\]
Then \[{T_2}\] becomes to left side = \[Ky\]
Restoring force = \[2{T_1} + 2{T_1} + {T_2}\]
= \[4{T_1} + {T_2}\]
= \[8Ky + Ky\]
= \[m{\omega ^2}y\] ∴ \[K = m{\omega ^2}\]
 Then, \[\omega = \sqrt {\dfrac{{9K}}{m}} \] =\[3\sqrt {\dfrac{K}{m}} \]
\[{T_1}\] + \[{T_2}\] = \[\dfrac{{4\pi }}{3}\sqrt {\dfrac{m}{K}} \]

So, the correct answer is “Option C”.

Note:
Swing and pendulum are the most common example of simple harmonic motion. In case of pendulum, pendulum oscillates in back and forth from its mean position. The process of hearing in living things is not possible without simple harmonic motion. Simple harmonic motion is important in oscillations. The mass \[M\] and force constant \[K\] are the only factors that affect the simple harmonic motion.