Question

A block of mass 50kg slides over a horizontal distance of 1m. If the coefficient of friction between their surfaces is 0.2, then work done against friction is:
A. 98J
B. 72J
C. 56J
D. 34J

Answer 1

Hint: Recall the expression for frictional force. Also draw a free body diagram to find the normal force acting on the block. After finding the frictional force by direct substitution recall the expression for work done. Now you could substitute the required quantities and hence find the work done against frictional force.

Formula used:
Expression for frictional force,
$F=\mu N$
Where ‘$\mu $’ is the coefficient of friction and N is normal force.
Expression for work done,
$W=F\times S$
here S is displacement.

Complete step by step answer:
In the question we are given a block of mass 50kg. We are sliding this block over a horizontal distance of 1m. We are given the coefficient of friction between the block and the surface. We are supposed to find the work done against this frictional force to slide this body. The situation is clearly shown in the figure below,

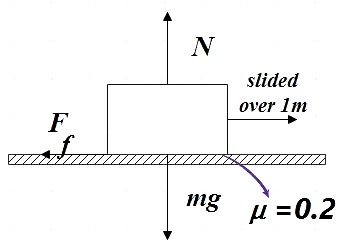
We know that frictional force is the opposition offered to the relative motion of between two objects. We have many types of friction, in this question we are dealing with dry friction which opposes relative lateral motion of two solid surfaces in contact. Dry friction is further divided into static and kinetic friction for non-moving and moving surfaces respectively.
Expression for kinetic friction here can be given by,
$F=\mu N$ …………………………….. (1)
Where, ‘$\mu $’ is the coefficient of friction and N is the normal force acting on the body.
From the diagram above we see that the normal force is equal to the weight of the body acting under the influence of gravity. That is,
$N=mg$
But, m =50kg
$g=9.8m{{s}^{-2}}$
$\Rightarrow N=50\times 9.8N$
$\Rightarrow N=490N$ ……………………………… (2)
Also we are given the value of coefficient of friction as,
$\mu =0.2$ ………………………….. (3)
Substituting (2) and (3) in (1), we get,
$\Rightarrow F=0.2\times 490N$
$\Rightarrow F=98N$ ……………………… (4)
But we are asked to find the work done against this force to move the block. We know that the expression for work done (W) is given by,
$W=F\times S$ …………………… (5)
Where, F = force
S = displacement
We are given,
$S=1m$ ………………….. (6)
Substituting (4) and (6) in (5) gives,
$W=98N\times 1m$
$W=98J$

So, the correct answer is “Option A”.

Note: In questions like this making a diagram with the given conditions helps you understand the question with better clarity. Doing so, helps you get the normal force on the block. Frictional force is a non-conservative force that is the work done against friction is path dependent.