Question

A block of mass 250g is kept on a vertical spring of spring constant 100N/m fixed from below. The spring is now compressed to have a length 10cm shorter than its natural length and the system is released from this position. How high does the block rise? (g=10$m{{s}^{-2}}$).
A. 10cm
B. 30cm
C. 20cm
D. 40cm

Answer 1

Hint: Calculate the work done by the spring force when it is under compression. Then calculate the work done by the spring force when the spring is under elongation. Find the work done by the gravity if the block rises by a height h. Then equate the total work done to the change in kinetic energy of the block.
Formula used:
${{W}_{s}}=\dfrac{1}{2}k{{x}^{2}}$
${{W}_{g}}=mgh$

Complete answer:
There are two forces acting on the block. One is the gravitational force exerted by the earth, which is always directed downwards. The second force is the spring force exerted by the spring.
As the block is released from the given position, since the spring is compressed, the spring will exert an upward force. At this point, the spring force is greater than the gravitational force. Hence, the block will rise up.
Since the displacement is along the direction of the spring force, the work done by the spring force is positive. The work done by a spring force is given as ${{W}_{s}}=\dfrac{1}{2}k{{x}^{2}}$, k is the spring constant of the spring and x is the compression or the extension in the spring.
It is given that the spring is compressed by 10cm. Therefore, the work done by the spring when it is compressed is ${{W}_{s,1}}=\dfrac{1}{2}k{{x}^{2}}=\dfrac{1}{2}(100){{(10)}^{2}}$.

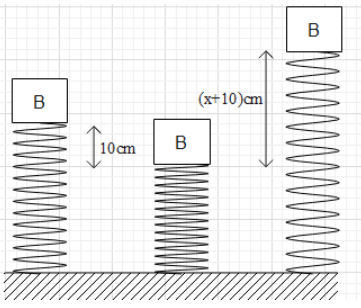
When the block rises above the natural length of the spring, the spring will elongate. As a result, the spring will exert a downward force. Therefore, now the spring will be doing negative work on the block.
Let the maximum extension in the spring be x. Therefore, the work done by the spring when it is elongated is ${{W}_{s,2}}=-\dfrac{1}{2}k{{x}^{2}}=\dfrac{1}{2}(100){{x}^{2}}$.
This means that block rises to height of $h=(x+10)cm$. The gravity will do a negative work because the gravitational force and the displacement of the block are in opposite directions.
The gravitational force will do a work of ${{W}_{g}}=-mgh$.
$\Rightarrow {{W}_{g}}=-(0.25kg)(10m{{s}^{-2}})h=-2.5h$
The total work done on the block is equal to the change in the kinetic energy of the block. In this case, the change in kinetic energy of the block is zero.
$\Rightarrow {{W}_{s,1}}+{{W}_{s,2}}+{{W}_{g}}=0$
$\Rightarrow \dfrac{1}{2}(100){{(10)}^{2}}-\dfrac{1}{2}(100){{x}^{2}}-2.5h=0$
$\Rightarrow 50\left( 100-{{x}^{2}} \right)-2.5h=0$
But, $x=h-10$
$\Rightarrow 50\left( 100-{{(h-10)}^{2}} \right)-2.5h=0$
$\Rightarrow 50\left( 100-({{h}^{2}}-20h+100) \right)-2.5h=0$
$\Rightarrow 20\left( 100-{{h}^{2}}+20h-100 \right)-h=0$
$\Rightarrow 2000-20{{h}^{2}}+400h-2000-h=0$
$\Rightarrow -20{{h}^{2}}+399h=0$.
$\Rightarrow h\left( -20h+399 \right)=0$
We know that h is not equal to zero.
$\Rightarrow \left( -20h+399 \right)=0$
$\Rightarrow h=\dfrac{399}{20}=19.95cm\approx 20cm$.

Hence, the correct option is C.

Note:
We can also find the maximum height of the block with the law of conservation of energy. According to the law of conservation of the energy, the sum of the potential energy and the kinetic energy of the particle is conserved.
This means that the sum of potential energy and kinetic energy at the time of release is equal to the sum of the potential energy and the kinetic energy at the highest point.
In this case, the potential energy will due to the gravitational force and the spring force.
The potential energy at height h from a reference point (where U=0) is given as U = mgh.
The potential energy when the change in length of the spring from its natural length is x is given as $U=\dfrac{1}{2}k{{x}^{2}}$