Question

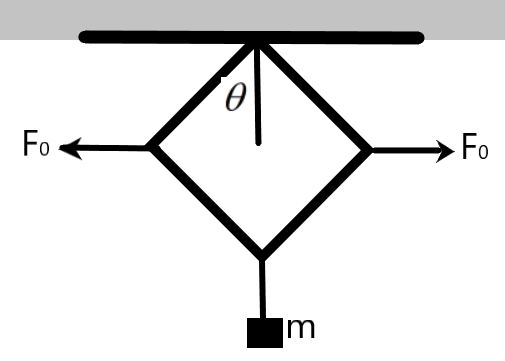
A block is suspended with the help of a frame made up of four tight rods each of length l. The mass of block is m. The block is kept in equilibrium by applying two forces \[{{F}_{0}}\]as shown in the figure. Find the time period of small vertical oscillations. In equilibrium rods make angle \[{{30}^{0}}\] with the vertical.
                         

\[\begin{align}
  & \text{A) 2}\pi \sqrt{\dfrac{3l}{g}} \\
 & \text{B) 2}\pi \sqrt{\dfrac{\sqrt{3}l}{4g}} \\
 & \text{C) 2}\pi \sqrt{\dfrac{\sqrt{3}l}{2g}} \\
 & \text{D) }\text{2}\pi \sqrt{\dfrac{3l}{\sqrt{2}g}} \\
\end{align}\]

Answer 1

Hint: We need to find the time period of oscillation of the system as given in the problem. We can find the effective length of the rods that will be affected by the oscillation due to the force provided at the two opposite sides of the frame as per the question.

Complete step by step solution:
We are given a situation in which four rigid rods, each of length ‘l’ are made into frame as shown in the figure. A block of mass ‘m’ hangs vertically downwards supported by the frame of rods. We need to evaluate the time period of the vertical oscillation of the system balanced horizontally by the opposite forces.
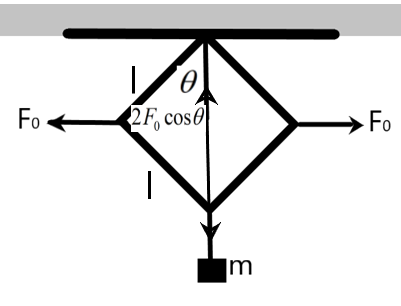
We can find the effective force which balances the system. We know that the system is balanced when the vertical angle is \[{{30}^{0}}\]. The vertical force balancing the mass of block is given as –
\[2{{F}_{0}}\cos \theta =mg\]
                     

\[\begin{align}
  & \text{but,} \\
 & \theta ={{30}^{0}} \\
 & \Rightarrow {{F}_{0}}=\dfrac{mg}{\sqrt{3}} \\
\end{align}\]
Now, we can find the effective length of the frame which undergoes the vertical oscillation due to the forces acting.
The given rhombus will have an effective vertical length along the line of force in vertical direction when the system is at equilibrium is given as –
\[\begin{align}
  & {{l}_{eff}}=l\cos \theta \\
 & \theta ={{30}^{0}} \\
 & \Rightarrow {{l}_{eff}}=l\dfrac{\sqrt{3}}{2} \\
 & \Rightarrow {{l}_{eff}}=\dfrac{\sqrt{3}l}{2} \\
\end{align}\]
Now, we can find the time period of the vertical oscillation as –
\[\begin{align}
  & T=2\pi \sqrt{\dfrac{{{l}_{eff}}}{g}} \\
 & \therefore T=2\pi \sqrt{\dfrac{\sqrt{3}l}{2g}} \\
\end{align}\]
The time period of oscillation is found to be \[T=2\pi \sqrt{\dfrac{\sqrt{3}l}{2g}}\].

So, the correct answer is “Option C”.

Note: The force acting on the mass to keep it balanced by horizontal forces will be in equilibrium in horizontal. But the vertical stability will not be attained in normal situations. The vertical oscillation is the result of this instability in the vertical direction.