Question

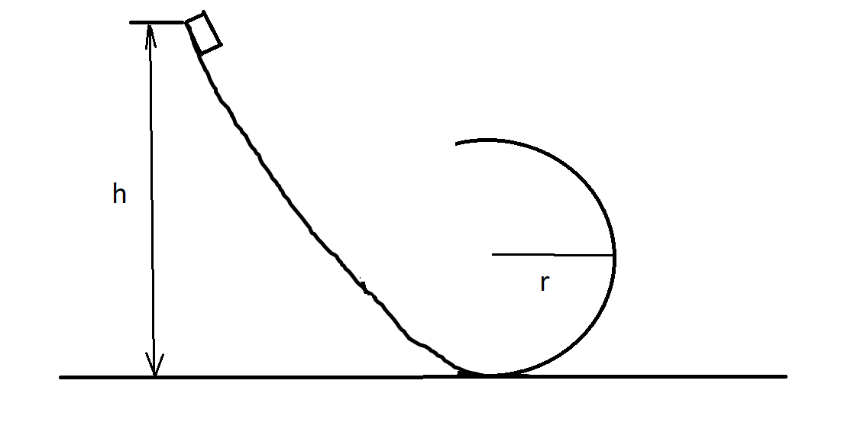
A block follows the path as shown in the figure from height h. If radius of circular path is r, then relation that holds good to complete full circle is

A. h < 5r/2
B. h > 5r/2
C. h = 5r/2
D. h $ \geqslant $ 5r/2

Answer 1

Hint: When the body has to maintain its motion along a circular path, it has to maintain a decent amount of velocity, so as to resist the force that pulls the object towards its centre, which is termed as the centripetal force.
Centripetal force, \[F = \dfrac{{m{v^2}}}{r}\]
where m = mass, v = velocity and r = radius of curvature of the circular path.

Complete step-by-step answer:
Consider the block of mass m which is dropped from the height h as shown.

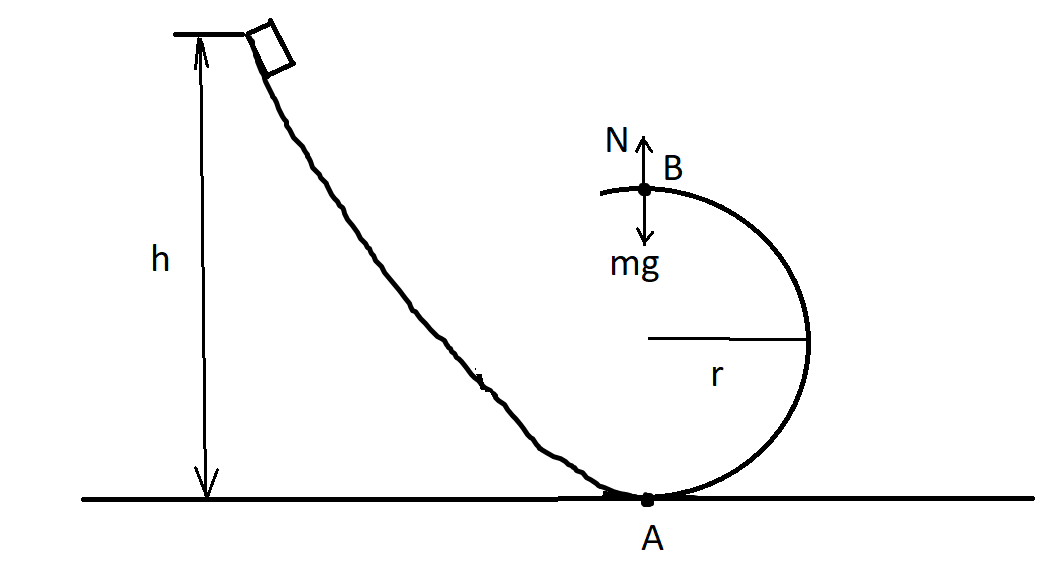
Let A be the lowest point and B be the highest point of the circular path of radius r.
The object will be able to reach the height to point B only if the normal force exceeds its own weight, thus overriding the centripetal force acting on the block towards the centre of the circular path.
Let ${v_B}$ be the velocity of the block at point B.
At point B, the centripetal force acting on the block will be the sum of weight and the normal force.
Centripetal force, \[\dfrac{{m{v^2}_B}}{r} = mg + N\]
To maintain the speed to reach to the top, the normal force must be in the positive direction adding up to the weight so that the necessary force can drive the block against the centripetal force.
Thus, N > 0.
Then we get –
\[
  \dfrac{{m{v^2}_B}}{r} = mg + N \\
   \to {v^2}_B = gr + N \\
   \to {v^2}_B > gr \\
 \]
When the block moves from point A to point B, there is an increase in the potential energy of the block and decrease in the kinetic energy of the block.
Due to conservation of mechanical energy, we have –
$
  KE + PE = 0 \\
   \to KE = - PE \\
 $
Kinetic energy change from B to A, $KE = \dfrac{1}{2}mv_B^2 - \dfrac{1}{2}mv_A^2$
Potential energy of the block at point B, $PE = mgh = mg(2r) = 2mgr$
Equating,
$
  KE = - PE \\
   \to \dfrac{1}{2}mv_B^2 - \dfrac{1}{2}mv_A^2 = - 2mgr \\
   \to \dfrac{1}{2}mv_A^2 - 2mgr = \dfrac{1}{2}mv_B^2 \\
   \to \dfrac{1}{2}mv_A^2 = \dfrac{1}{2}mv_B^2 + 2mgr \\
 $
Applying the condition \[{v^2}_B > gr\], we get –
$\dfrac{1}{2}mv_A^2 > \dfrac{1}{2}mv_B^2 + 2mgr$
Substituting, \[{v^2}_B = gr\]
$
  \dfrac{1}{2}mv_A^2 > \dfrac{1}{2}mgr + 2mgr \\
   \to \dfrac{1}{2}mv_A^2 > \dfrac{5}{2}mgr \\
 $
Now, we will calculate the velocity of the block at point A, i.e. ${v_A}$.
When the block falls from the height h, the potential energy of the block at that height gets converted into kinetic energy. Applying the energy equation, we get –
$
  KE = - PE \\
   - \dfrac{1}{2}mv_A^2 = - mgh \\
   \to \dfrac{1}{2}mv_A^2 = mgh \\
 $
Substituting in the equation above, we get –
$
  \dfrac{1}{2}mv_A^2 > \dfrac{5}{2}mgr \\
  mgh > \dfrac{5}{2}mgr \\
  \therefore h > \dfrac{{5r}}{2} \\
 $

Thus, the correct option is Option B.

Note: The centripetal force is a force that directs the body towards the centre. However, there is another equal and opposite force acting on the body that pushes the body away from the centre and thus, keeps the body moving constantly, in the circular path. This force is called the centrifugal force.
Centrifugal force = $ - $ Centripetal force
This keeps the necessary balance of the body moving in the circular path.