Question

A binary star system consists of two stars of masses ${{M}_{1}}$ and ${{M}_{2}}$ revolving in circular orbits of radii ${{R}_{1}}$ and ${{R}_{2}}$ respectively. If their respective time periods are ${{T}_{1}}$ and ${{T}_{2}}$, then
$A){{T}_{1}}>{{T}_{2}}$ if ${{R}_{1}}>{{R}_{2}}$
$B){{T}_{1}}>{{T}_{2}}$ if ${{M}_{1}}>{{M}_{2}}$
$C){{T}_{1}}={{T}_{2}}$
$D)\dfrac{{{T}_{1}}}{{{T}_{2}}}={{\left( \dfrac{{{R}_{1}}}{{{R}_{2}}} \right)}^{\dfrac{3}{2}}}$

Answer 1

Hint: The point around which the stars in the binary star system revolve acts as the centre of mass of the system. By the property of the centre of mass, the product of mass and radius of one star in the binary star system is equal to the product of mass and radius of the other star. Also, gravitational force between the two stars in the binary star system is equal to the centripetal force acting on each star.

Formula used:
$1){{M}_{1}}R{}_{1}={{M}_{2}}{{R}_{2}}$
$2){{F}_{g}}=\dfrac{G{{M}_{1}}{{M}_{2}}}{{{R}^{2}}}$
$3){{F}_{c}}=\dfrac{M{{V}^{2}}}{R}$
$4){{F}_{g}}={{F}_{c}}$

Complete step by step answer:
We are provided with a binary star system, consisting of two stars of masses ${{M}_{1}}$ and ${{M}_{2}}$ revolving in circular orbits of radii ${{R}_{1}}$ and ${{R}_{2}}$ respectively. It is also given that their respective time periods of revolution are ${{T}_{1}}$ and ${{T}_{2}}$. Firstly, let us call the stars in the binary star system $A$ and $B$, respectively, as shown in the figure.

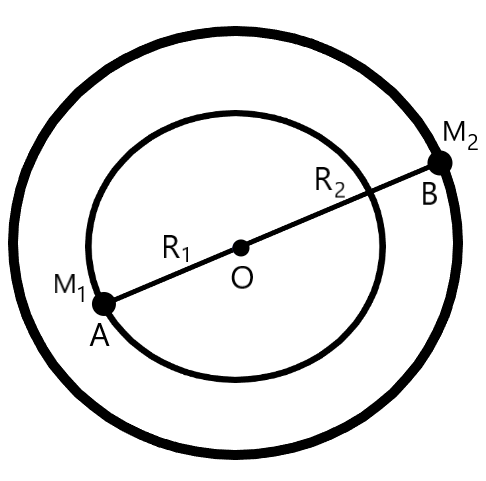
The point around which both the stars in the binary star system revolve acts as the centre of mass of the system. Clearly, in the given figure, $O$ acts as the centre of mass of both the stars $A$ and $B$. From the definition of centre of mass of a binary system, we have
${{M}_{1}}R{}_{1}={{M}_{2}}{{R}_{2}}$
where
${{M}_{1}}$ is the mass of star $A$, as shown in the figure
${{R}_{1}}$ is the radius of the star $A$
${{M}_{2}}$ is the mass of star $B$, as shown in the figure
${{R}_{2}}$ is the radius of the star $B$
Let this be equation 1.
Now, force of gravitation between star $A$ and star $B$ is given by
${{F}_{g}}=\dfrac{G{{M}_{1}}{{M}_{2}}}{{{R}^{2}}}$
where
${{F}_{g}}$ is the gravitational force between star $A$ and star $B$
$G$ is the gravitational constant
${{M}_{1}}$ is the mass of star $A$
${{M}_{2}}$ is the mass of star $B$
$R={{R}_{1}}+{{R}_{2}}$ is the distance between star $A$ and star $B$
Let this be equation 2.
Another force which acts on each star is centripetal force, which keeps each star revolving around $O$. If ${{F}_{c1}}$ represents the centripetal force acting on star $A$, then, ${{F}_{c1}}$ is given by
${{F}_{c1}}=\dfrac{{{M}_{1}}{{V}_{1}}^{2}}{{{R}_{1}}}$
where
${{F}_{c1}}$ is the centripetal force acting on star $A$
${{M}_{1}}$ is the mass of star $A$
${{R}_{1}}$ is the radius of the star $A$
${{V}_{1}}$ is the velocity of star $A$
Let this be equation 3.
Similarly, if ${{F}_{c2}}$ represents the centripetal force acting on star $B$, then, ${{F}_{c2}}$ is given by
${{F}_{c2}}=\dfrac{{{M}_{2}}{{V}_{2}}^{2}}{{{R}_{2}}}$
where
${{F}_{c2}}$ is the centripetal force acting on star $B$
${{M}_{2}}$ is the mass of star $B$
${{R}_{2}}$ is the radius of the star $B$
${{V}_{2}}$ is the velocity of star $B$
Let this be equation 4.
Now, for the binary system of stars to be stable, we know that all these forces acting on each star should be equal. Therefore, we can equate equation 2, equation 3 and equation 4, as follows:
\[\begin{align}
& {{F}_{g}}={{F}_{c1}}\Rightarrow \dfrac{G{{M}_{1}}{{M}_{2}}}{{{R}^{2}}}=\dfrac{{{M}_{1}}{{V}_{1}}^{2}}{{{R}_{1}}} \\
& {{F}_{g}}={{F}_{c2}}\Rightarrow \dfrac{G{{M}_{1}}{{M}_{2}}}{{{R}^{2}}}=\dfrac{{{M}_{2}}{{V}_{2}}^{2}}{{{R}_{2}}} \\
& {{F}_{c1}}={{F}_{c2}}\Rightarrow \dfrac{{{M}_{1}}{{V}_{1}}^{2}}{{{R}_{1}}}=\dfrac{{{M}_{2}}{{V}_{2}}^{2}}{{{R}_{2}}} \\
\end{align}\]
Let this be equation 5.
Here, we know that
${{V}_{1}}=\dfrac{2\pi {{R}_{1}}}{{{T}_{1}}}$
and
${{V}_{2}}=\dfrac{2\pi {{R}_{2}}}{{{T}_{2}}}$
where
${{V}_{1}}$ is the velocity of star $A$
${{V}_{2}}$ is the velocity of star $B$
${{R}_{1}}$ is the radius of star $A$
${{R}_{2}}$ is the radius of star $B$
${{T}_{1}}$ is the time period of star $A$
${{T}_{2}}$ is the time period of star $B$
Let this set of equations be denoted by X.
Substituting the set of equations denoted by X in equation 5, we have
\[\dfrac{{{M}_{1}}{{V}_{1}}^{2}}{{{R}_{1}}}=\dfrac{{{M}_{2}}{{V}_{2}}^{2}}{{{R}_{2}}}\Rightarrow \dfrac{{{M}_{1}}{{\left( \dfrac{2\pi {{R}_{1}}}{{{T}_{1}}} \right)}^{2}}}{{{R}_{1}}}=\dfrac{{{M}_{2}}{{\left( \dfrac{2\pi {{R}_{2}}}{{{T}_{1}}} \right)}^{2}}}{{{R}_{2}}}\Rightarrow \dfrac{4{{\pi }^{2}}{{R}_{1}}{{M}_{1}}}{{{T}_{1}}}=\dfrac{4{{\pi }^{2}}{{R}_{2}}{{M}_{2}}}{{{T}_{2}}}\Rightarrow \dfrac{{{M}_{1}}{{R}_{1}}}{{{T}_{1}}}=\dfrac{{{M}_{2}}{{R}_{2}}}{{{T}_{2}}}\]

Let this be equation 6.
Using equation 1 in equation 6, we have
\[\dfrac{{{M}_{1}}{{R}_{1}}}{{{T}_{1}}}=\dfrac{{{M}_{2}}{{R}_{2}}}{{{T}_{2}}}\Rightarrow \dfrac{1}{1}=\dfrac{{{T}_{1}}}{{{T}_{2}}}\Rightarrow {{T}_{1}}={{T}_{2}}\]
This result suggests that time periods of revolution of both the stars in the given binary system of stars are equal.
Therefore, the correct answer is option $C$.

Note:
Students need not get confused with the derivation given by equation 5. Equation 5 is nothing but a consequence of Kepler’s third law of planetary motion, which states that
${{T}^{2}}\propto {{R}^{3}}$
where
$T$ is the time period of revolution of a celestial body
$R$ is the orbital radius of the celestial body
This expression looks very similar to option $D$ and can cause confusion. Here, students need to understand that ${{T}_{1}}={{T}_{2}}$ and that substituting this equation in the last option gives
$\dfrac{{{T}_{1}}}{{{T}_{2}}}={{\left( \dfrac{{{R}_{1}}}{{{R}_{2}}} \right)}^{\dfrac{3}{2}}}\Rightarrow 1={{\left( \dfrac{{{R}_{1}}}{{{R}_{2}}} \right)}^{\dfrac{3}{2}}}\Rightarrow {{R}_{1}}={{R}_{2}}$
which contradicts the assumptions put forward by the question. Therefore, option $D$ is incorrect.