Question

A bicycle is running straight towards the north. What is the locus of the centre of the front wheel of the bicycle whose diameter is d?
A.A line parallel to the path of the wheel of the bicycle at a height d cm
B.A line parallel to the path of the wheel of the bicycle at a height \[\dfrac{d}{2}\] cm
C.A circle of radius \[\dfrac{d}{2}\]cm
D.A circle of radius d cm

Answer 1

Hint:
The path traced by a moving point under some geometrical condition or conditions is called its locus.
So, for the locus of given question, we have to observe the path traced by the centre of the front wheel of the bicycle.

Complete step by step solution:
When a point moves so as always to satisfy a given condition, or a set of conditions, the path it traces out is called its locus.
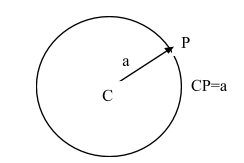
Example- Suppose C be a given point and a point P in the rectangular Cartesian plane moves in such a way that its distances from C remains constant and equal to a (i.e. CP=a). Clearly the moving point must lie on the circumference of a circle whose centre is C and radius is a. Therefore the locus of P in the given condition is the circumference of this circle. But in a given condition when the bicycle is running straight forward towards north the centre of the front wheel of the bicycle moves on a line parallel to the path of the wheel of the bicycle at height d/2 cm.

Therefore, the locus of the centre of the front wheel of the bicycle is a line parallel to the path of the wheel of the bicycle at a height \[\dfrac{d}{2}\]cm.
∴ Option (B) is correct.

Note:
Students should observe the path traced by the moving point under given conditions.
This can be evaluated with the help of algebraic relations. This algebraic relation is called the equation of the circle.