Question

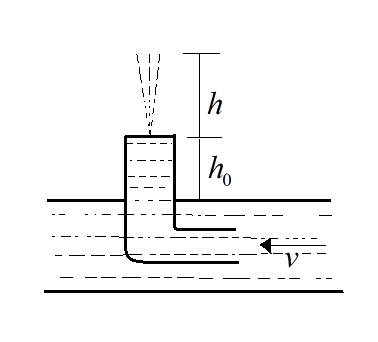
A bent tube is lowered into a water stream as shown in figure shown above. The velocity of the stream relative to the tube is equal to \[v=2.5m{{s}^{-1}}\]. The closed upper end of the tube located at the height \[{{h}_{0}}=12cm\] has a small orifice. The height h (in cm) the water jet spurt is \[2\times {{10}^{x}}\]. Find \[x\].

Answer 1

Hint: The water coming in the tube with a certain velocity, went out through orifice. It follows the energy conservation law. The kinetic energy due to velocity v is converted into potential energy, and this kinetic energy is used to raise the water to height h.

Complete step by step answer:
In hydrodynamics Bernoulli had derived the equation for energy conservation law; which states that energy is neither created nor destroyed. It changes from one form to another form.
By Bernoulli’s Theorem:
\[P+\rho gh+\dfrac{1}{2}\rho {{v}^{2}}=\]Constant
Where:
\[P=\]Atmospheric pressure
\[\rho =\]density of fluid
\[h=\] height above the surface
\[v=\]velocity of fluid
In our question atmospheric pressure inside the tube is zero.
Therefore we apply Bernoulli’s Theorem at the entering point (where water enters into the tube) and at the end point (or orifice) from where water ejects.
\[\begin{align}
  & \dfrac{1}{2}\rho {{v}_{in}}^{2}=\dfrac{1}{2}\rho {{v}^{2}}_{out}+\rho g{{h}_{0}} \\
 & {{v}^{2}}_{out}={{v}_{in}}^{2}-2g{{h}_{0}} \\
\end{align}\]
This is the velocity that comes out from orifice.
Now again applying energy conservation law, so that water can jump to height h.
Total Initial Energy = Total Final Energy
\[\begin{align}
  & \dfrac{1}{2}m{{v}_{out}}^{2}=mgh \\
 & {{v}^{2}}_{out}=gh \\
 & {{v}_{in}}^{2}-2g{{h}_{0}}=gh \\
 & h=\dfrac{{{v}_{in}}^{2}-2g{{h}_{0}}}{2g} \\
\end{align}\]
Putting the values of all parameters in the above equation, we get
\[\begin{align}
  & h=\dfrac{{{2.5}^{2}}-2\times 9.8\times 12\times {{10}^{-2}}}{2\times 9.8} \\
 & h=0.20m \\
 & h=2\times 10cm \\
\end{align}\]
Comparing this height with the question height we can find the value of x
\[2\times 10=2\times {{10}^{x}}\]
\[\]
Hence, the height through which the water rises is 20cm. And by comparing the height of the above equation, we find that x must be equals to 1.

Note: Sometimes students forget to put the SI units, for example if height is given in cm first change it into meters then find the answer.
To find height or to find velocity we always use energy conservation law.