Question

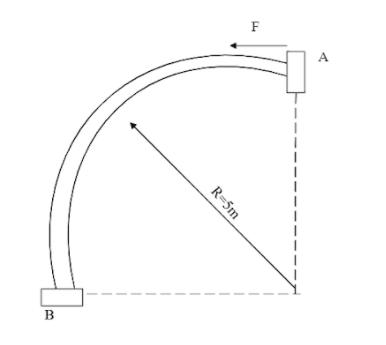
A bead of mass $1/2kg$ starts from rest from A to move in a vertical plane along a smooth fixed quarter ring of radius $5m$ , under the action of a constant horizontal force $F = 5N$ as shown in the figure. The speed of bead as it reaches point B is:

A.$14.14m{s^{ - 1}}$
B.$7.07m{s^{ - 1}}$
C.$5m{s^{ - 1}}$
D.$25m{s^{ - 1}}$

Answer 1

Hint: Work is a form of energy that is transferred to or from an object using force as a medium to move the object through a distance. Mathematically work can be represented as the product of force and displacement.
$W = F \times s$
We know that work is closely related to energy and energy of a system at all times should be conserved. Thus, by work-energy principle we can say that the work done on a body is equivalent to the change in kinetic energy of the body.
$W = \Delta KE$
Formulas used:
We will be using the formula to find the kinetic energy of a body, $KE = \dfrac{1}{2}m{v^2}$ where $KE$ is the kinetic energy of the body, $m$ is the mass of the body, and $v$is the velocity of the body.
We will also be using the formula $W = F \times s$ where $W$is the work done by the body, $F$ is the force applied on the body to move through a displacement of $s$ .

Complete answer:
We know that energy of a system is always conserved and work done by a body is the energy possessed by the body. We can infer from the problem that the body is required to move through a circular arc of radius $R = 5m$ and the mass of the body, $m = 0.5kg$ .

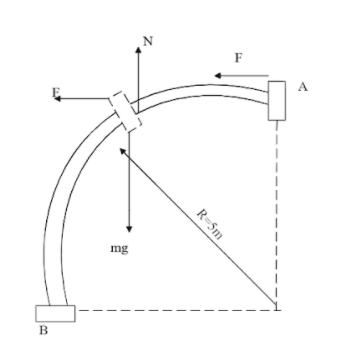
We shall consider that the body has travelled a certain distance along the circular arc from A, now the body has 3 forces acting on it. The gravitational force that pulls the body towards the earth, the normal force that acts perpendicular to the surface, and the constant force applied by the body.
We also know that the total work done in a system is equal to the change in kinetic energy of the system. $W = \Delta KE$ . We also know that the body is starting from rest thus the initial velocity will be zero, so will be the initial kinetic energy.
$\Delta KE = \dfrac{1}{2}m{v^2} - \dfrac{1}{2}m{\left( 0 \right)^2}$
Now we know the forces acting on the body, let us calculate the work done due to each force. We know that work is the product of force and distance. Thus, the work done by gravity in moving the body from A to B will be, ${W_{mg}} = mgR$ [Since the body’s displacement in the downward direction is $R$ ]
Similarly, the work done on the body due to the constant force applied is ${W_F} = F \times R$ [Since the body’s displacement in the horizontal direction is $R$]
The work done by the body due to the normal force acting upwards is zero, because the body does not move in the upward direction.
So, equating the total work done to the change in kinetic energy we get,
${W_{mg}} + {W_F} + {W_N} = \Delta KE$
$mgR + \left( {F \times R} \right) + 0 = \dfrac{1}{2}m{v^2} - \dfrac{1}{2}m{\left( 0 \right)^2}$
Substituting the known values of $m,g,R,F$ and solving we get,
$\left( {0.5 \times 10 \times 5} \right) + \left( {5 \times 5} \right) + 0 = \dfrac{1}{2} \times 0.5 \times {v^2}$
$50 = \dfrac{1}{2} \times 0.5 \times {v^2}$
Solving for $v$ we get,
${v^2} = 200$
$ \Rightarrow v = \sqrt {200} = 14.14m/s$
Thus, the speed of the particle is $v = 14.14m/s$ .

Hence the correct answer will be option A.

Note:
In this system when the body is at rest the kinetic energy of the body is converted into potential energy. Thus the energy of the system is always conserved in this system.