Question

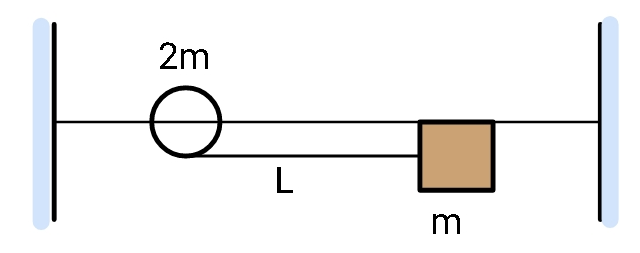
A bead can slide on a smooth straight wire and a particle of mass m is attached to the bead by a light string of length L. The particle is held in contact with the wire with the string taut and is then let to fall. If the bead has the mass 2m, then when the string makes an angle $\theta$ with the wire the bead will have slipped a distance:

A. $L (1- \cos \theta)$
B. $\dfrac{L}{2} (1- \cos \theta)$
C. $\dfrac{L}{3} (1- \cos \theta)$
D. $\dfrac{L}{6} (1- \cos \theta)$

Answer 1

Hint: The bead is constrained to move along horizontal direction only. The block is made to fall under the action of gravity. In the absence of any external force, a system remains unchanged. There is no force acting along horizontal direction on the system.

Complete answer:
Assume the bead resting at origin initially and the block resting at some L (x coordinate). We may say that initially, the momentum is zero for the system. So, the same applies to the centre of mass. Centre of mass of a system behaves like a single particle which defines the entire system.
So we may write:
$MV_{CM} =0$ for final and initial case.
$\dfrac{dx_i}{dt} = 0 = \dfrac{dx_f}{dt} $
Integrating this we get:
$\Delta x= 0$
$x_f = x_i $
Or
Therefore the displacement of the centre of mass along x direction will give us our required distance that the bead will travel. So, we can just find initial and final x coordinates of the centre of mass and equate them.

Initially the position of centre of mass when bead has x=0 and block has x=L, is:
$x_i = \dfrac{0 + m. L}{2m + m} = \dfrac{L}{3}$
Finally, the bead moves by a distance x on the x-axis and the block has x- coordinate that will depend on the angle that it makes with the x axis (see the right angled triangle):

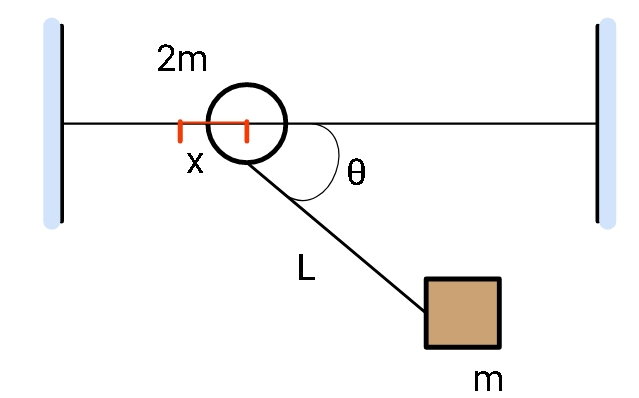
For block: x-coordinate = x+ $L \cos \theta$

Since the bead moves the distance x the block has to do the same therefore we added x to $L \cos \theta$

Therefore, our centre of mass has final x-coordinate:
$x_f = \dfrac{2m.x+ m. (x+ L \cos \theta)}{2m + m}$
Simplifying this and, equating the final and initial coordinates we get:
$ \dfrac{L}{3} = x + \dfrac{L \cos \theta}{3}$
Or we may write:
$ \dfrac{L(1- \cos \theta)}{3} = x $

So, the correct answer is “Option C”.

Note:
We have applied the law of conservation of momentum in the x direction. Because no external forces were acting along the x- direction, the change in momentum was supposed to be zero, also given by Newton's second law. Along the y- direction the case becomes different. Force of gravity serves as an external force along the y- axis and appears due to weight mg of the block.